Some algorithms and data structures from "Algoritmi e principi dell'informatica" course at Politecnico di Milano
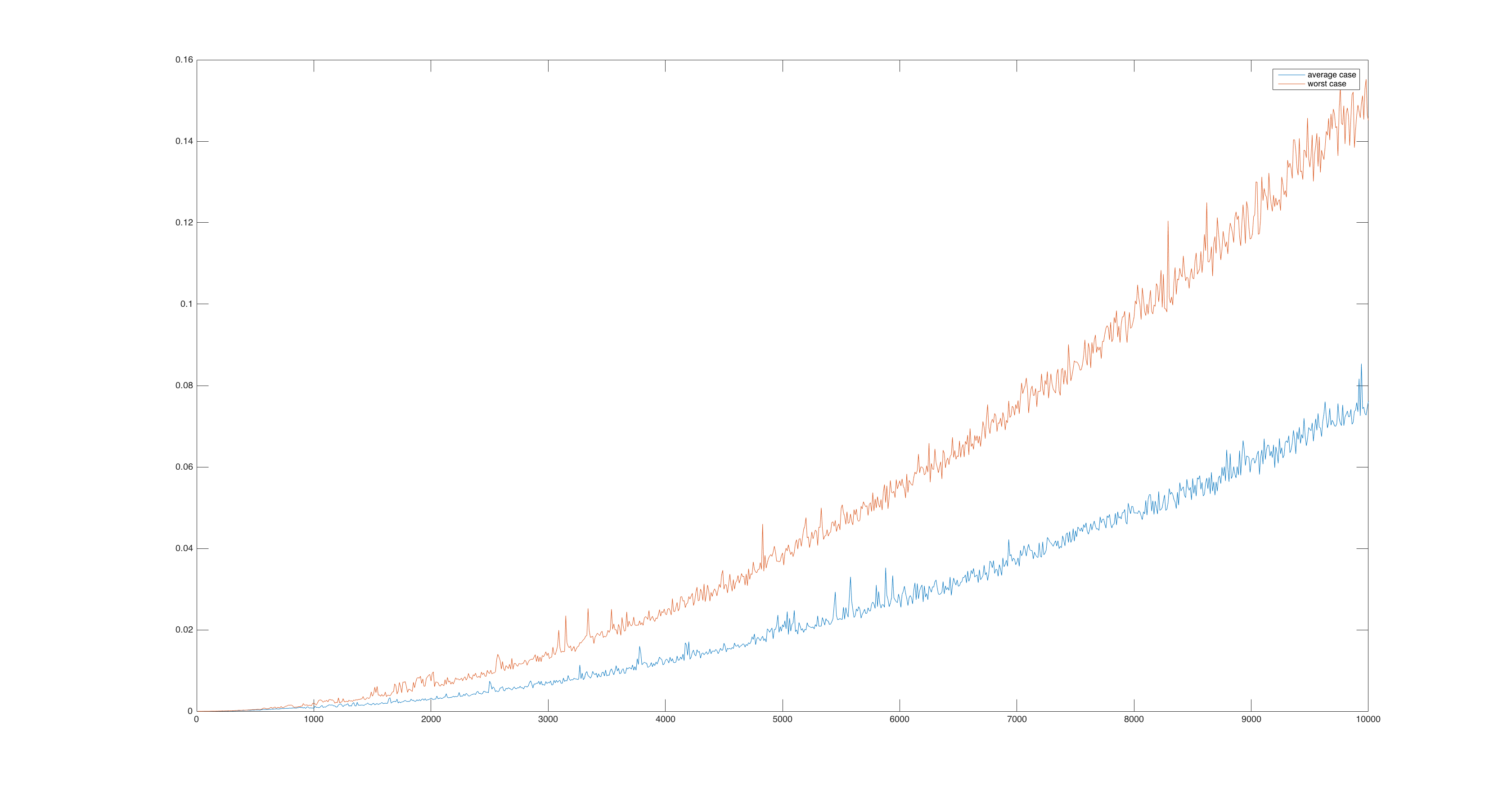
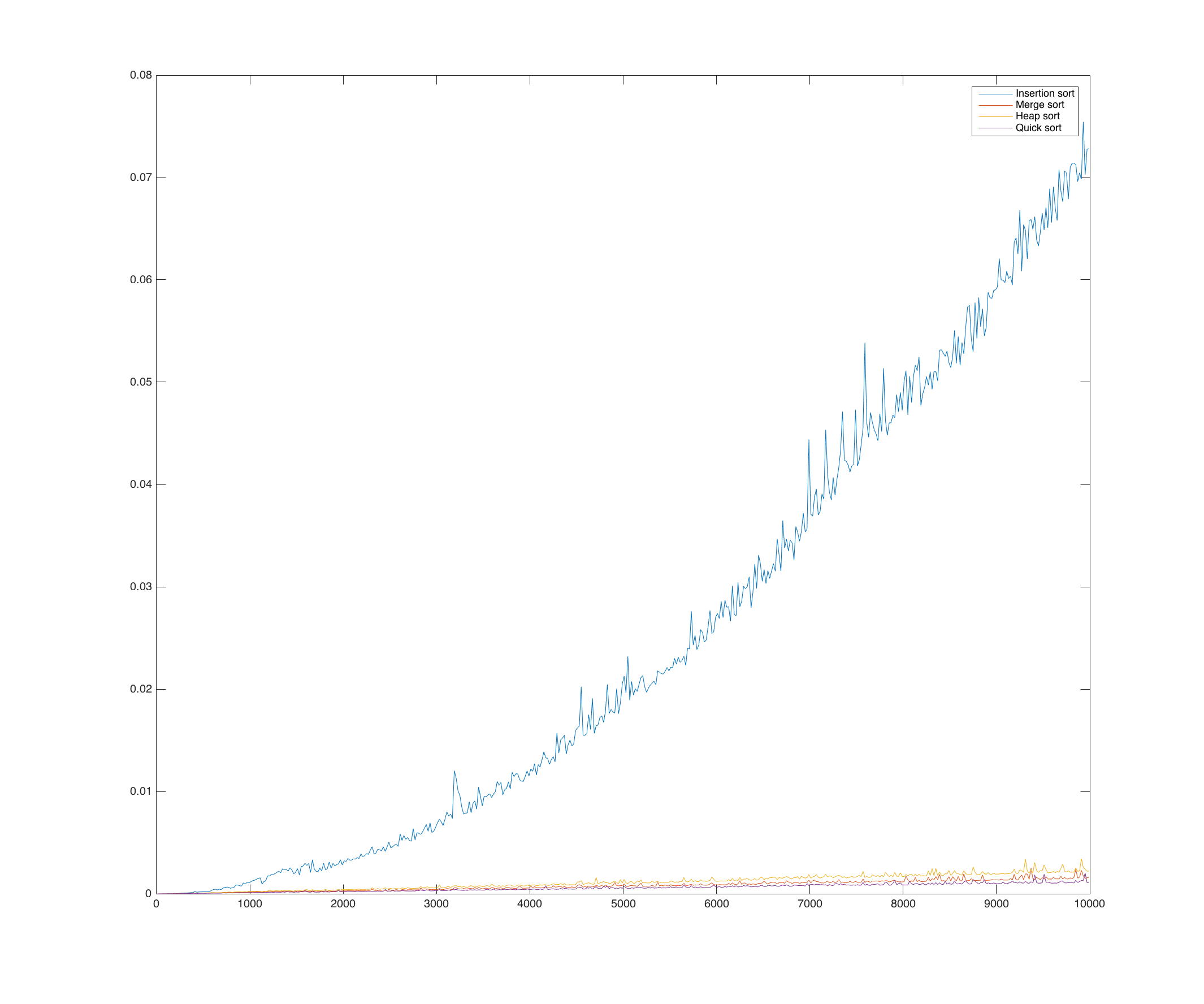
Just a simple comparison of the growing of temporal complexity of the most commons sorting algorithms at the growing of input size.
Insertion sort is a sorting algorithm efficient when the input is small, in fact the growth of the computation time is proportional to the square of the input length: T(n)=𝛩(n^2) where n is the length of the input array.
Merge sort is based on divide et impera paradigma:
Divide: the problem is recursively divided in two subproblems, each has half the complexity of the previous;
Impera: we recursively split the problem until the subproblem is banal and we can solve in one step;
Combina: the MERGE procedure combines the subproblems to solve the initial problem.
The time complexity is 𝛩(n*lg(n)).
Heap sort builds a binary tree where every node is higher or equal than its child, then it puts the root (higher element) at the last position of the array (l position), then it re-builds the tree with the remaining objects and puts the root at the l-1 position and so on until the entirely array is sorted.
The time complexity is O(n*lg(n)) and the memory used by this algorithm is only the memory needed to store the input array.
Like Merge sort, Quick sort is based on divide et impera paradigma:
Divide: to split the A[p..r] array into two subarrays A[p..q-1] and A[q+1..r] where each A[p..q-1] element is lower or equal than A[q] and each A[q+1..r] element is higher or equal than A[q];
Impera: sort the two sub-arrays by recursively applying the quicksort algorithm;
Combina: because of the two subarrays are allready sorted, the original array is allready sorted.
The time complexity in the worst case is 𝛩(n^2), but with a linear distributed input, the algorithm is executed in 𝛩(n*lg(n).
An implementation of the main functions of some data structures: lists, queues, stacks, binary search trees (BST) and red-black trees (RBT).
Breadth-first search (BFS) and Depth-first search (DFS) graph exploration.