by David Veenman (University of Amsterdam)
Comments/feedback welcome
bootstep is a program that can be used to obtain bootstrapped standard errors when the predicted values from a first-step estimation are used as independent variable in a second-step estimation. A shown in prior work, ignoring the sampling error of the generated regressor causes the second-step standard errors to be understated in the second-step estimation (see Pagan 1984 and Murphy and Topel 1985; see Chen et al. (2023) for illustrations in accounting/finance research). The procedure allows for estimation of standard errors that are robust to clustering in one or two dimensions using a pairs-cluster bootstrap approach and the formula for twoway cluster-robust standard errors from Thompson (2011) and Cameron, Gelbach, and Miller (2011). The program is largely based on Mata functions, which allows for fast execution of the bootstrap resampling procedure. To limit the effects of downward bias in standard errors with a small number of clusters (G), the program applies a small sample correction to the variance matrix and relies on critical values based on t(G-1) following the guidance of Cameron and Miller (2015).
The program can be installed by simply saving the *.ado file into your local Stata directory that contains additional ado programs. To identify this folder, type and execute "sysdir" in your Stata command window and go to the folder listed at "PLUS:". Make sure you place the program in the folder with the correct starting letter of the program (i.e., the folder named "b") and the file extension is correctly specified as *.ado.
The program requires the latest versions of moremata to be installed in Stata:
ssc inst moremata, replace
Version history and changes:
2024dec17 (version 1.2.1): Added residual option to include first-step residuals in second-stage estimation and removed standardize option
2024nov21 (version 1.2.0): Added Cameron/Gelbach/Miller (2011) adjustment for non-positive-semidefinite VCE
2023jan06 (version 1.1.1): minor update
2022dec16 (version 1.1.0):
- major update with fast execution in Mata now as default, including absorption of one-dimensional fixed effects
2021dec29 (version 1.0.2):
- fixed issue with fast option in combination with twoway clustering.
2021dec28 (version 1.0.1):
- added option "fast" for much faster bootstrap execution using mata.
- improved inference by adding the small sample correction to the variance matrix and using critical values based on t(G-1) following Cameron and Miller (2015).
2021dec03 (version 1.0.0):
- first commit to Github.
Syntax:
depvar1 indepvars1 | depvar2 indepvars2, options
- depvar1 is the first-step dependent variable;
- indepvars1 is/are the first-step independent variable(s);
- The vertical bar (|) separates the first and second step estimations;
- depvar2 is the second-step dependent variable;
- indepvars2 is/are the first-step independent variable(s).
Program options:
- nboot (required): number of bootstrap replications. Recommendation: use at least 1000 replications for precise inference.
- cluster(varlist) (optional): allows for bootstrap estimation of cluster-robust standard errors in one or two dimensions.
- logit (optional): allows the first step to be estimated using logit (provided the first-step dependent variable is an indicator variable); the first-step fitted values are transformed into predicted probabilities.
- absorb (optional): allows for one dimension of fixed effects to be absorbed in the second-step estimation.
- residual (optional): additionally include first-step residuals as variable in second-step estimation.
- seed (optional): sets the seed to ensure reproducibility of the results. Not required but highly recommended when seed is not set outside of the program.
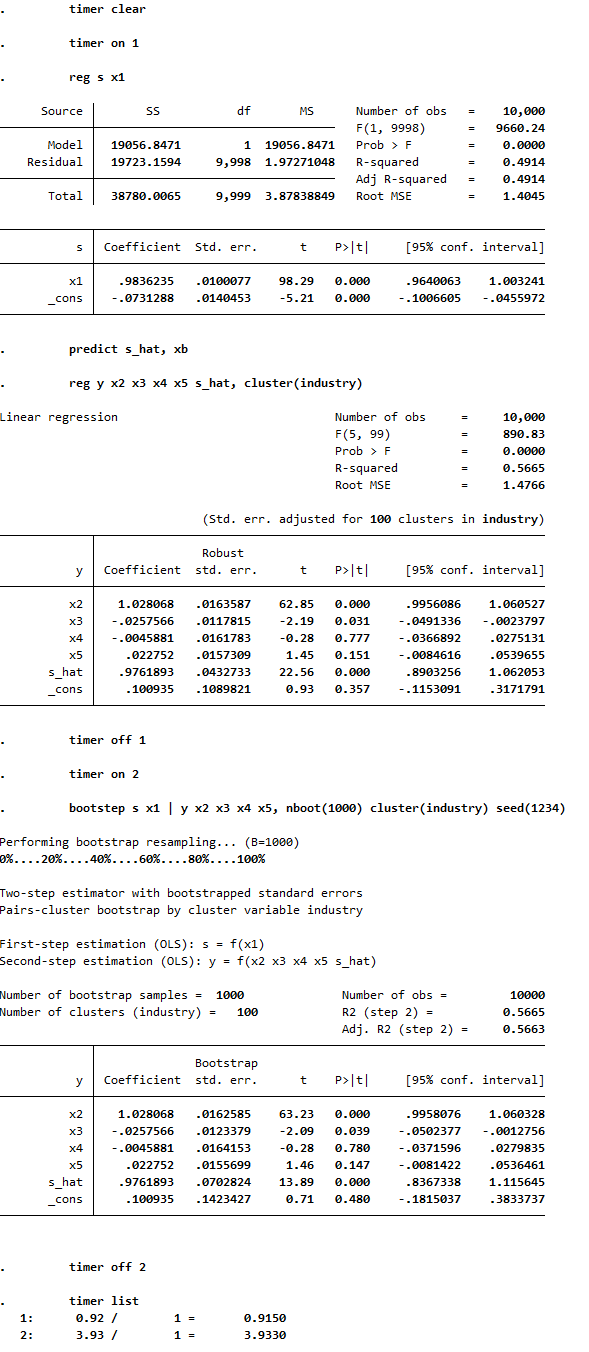
The following example shows how the program can be run and how fast it is (the program can be tested using the test_bootstep.do file). In the second-step OLS estimation with basic standard errors, the standard error of the coefficient on s_hat is too low and t-stat is too high compared to the unbiased bootstrap estimate. The screenshot also illustrates how performing 1000 bootstrap replications takes only about 4 seconds in this example:
The following output illustrates the biasedness and unbiasedness of the OLS and bootstrapped standard errors, respectively. These results can be replicated using the test_bootstep_sim.do file. Compared to the true standard errors (derived from the standard deviations of the coefficient estimates from 1000 simulated samples), the OLS standard errors are too low and the bootstrapped standard errors are very close. This results in type 1 error rates of 0.165 and 0.045, respectively, based on a significant level of 0.05:
. tabstat b_* se_* sig_*, stats(mean sd)
Stats | b_ols b_boot~p se_ols se_boo~p sig_ols sig_bo~p
---------+------------------------------------------------------------
Mean | 1.001036 1.001036 .0499406 .0711964 .165 .045
SD | .0712532 .0712532 .0064542 .0101848 .3713663 .2074079
----------------------------------------------------------------------
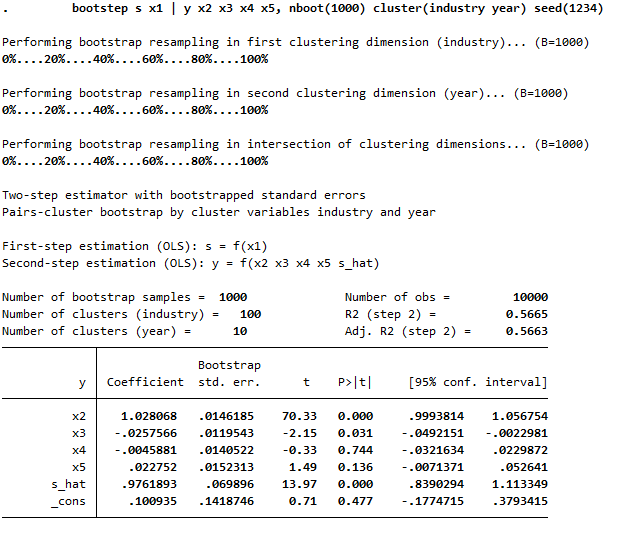
Example with two-way clustering:
Example without clustering:
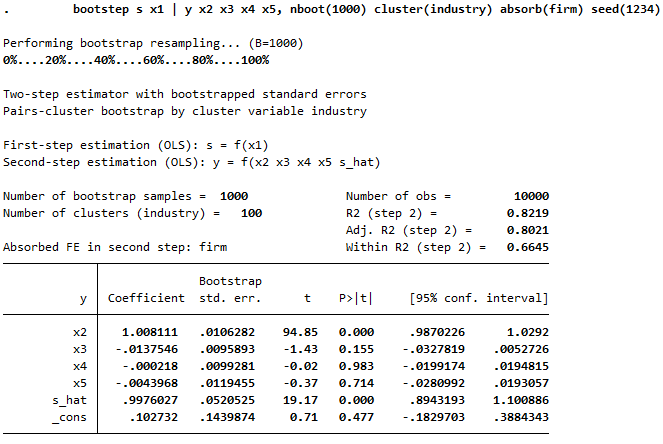
Example absorbing fixed effects in step 2:
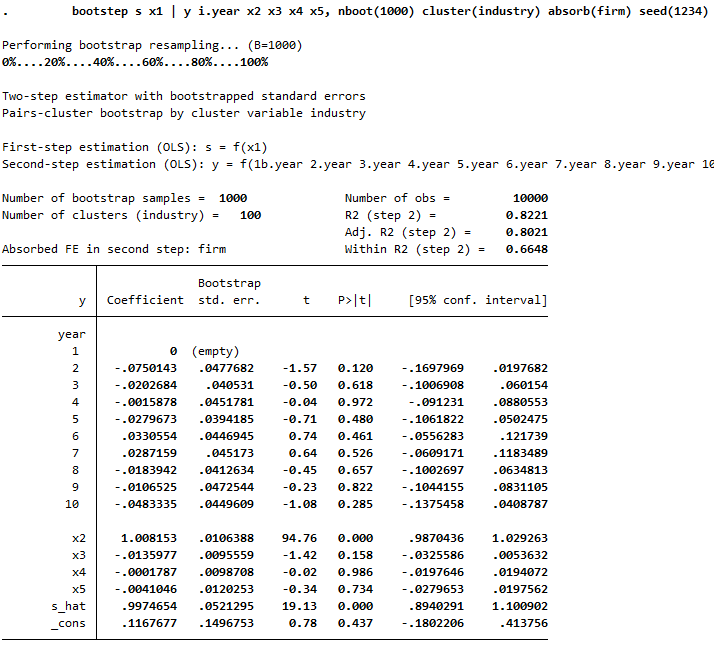
Example absorbing fixed effects and additional factor variables in step 2:
Additionally including first-step residuals in step 2: