A Time-Delay Estimation algorithm for Event Time-Series.
This package performs a time-delay estimation (TDE) between two event-based time-series that are relatively shifted by an unknown time offset. An event-based time-series is given by a set of sorted timestamps of certain events, e.g., heart beats or steps.
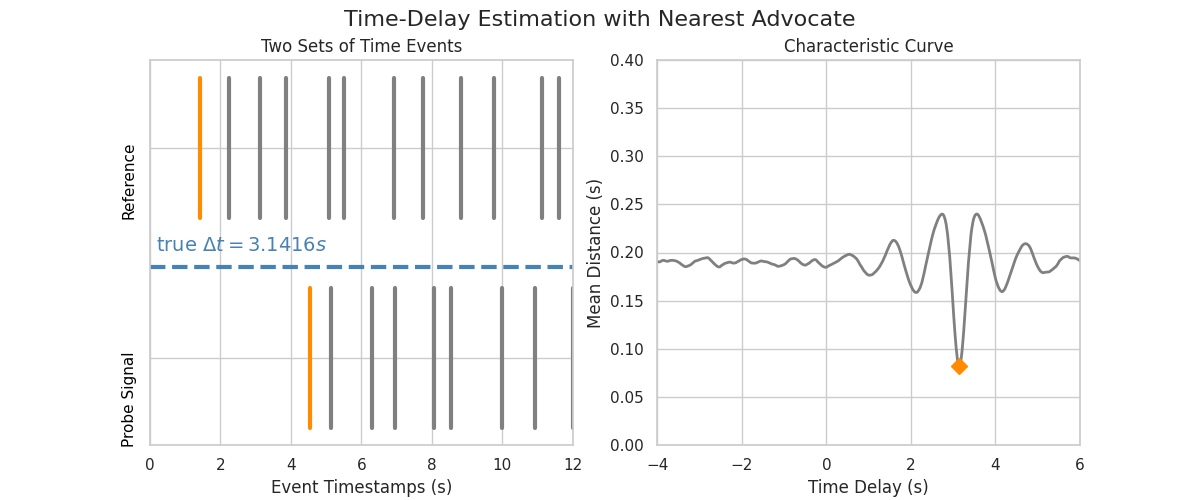
The Nearest Advocate algorithm is precise time-delay estimation in arrays of timestamps that is robust against noisy timestamps, a high fraction of missing events, and clock drift (Schranz et al., 2024).
Time-delay estimation is also called correction of time offsets, time lags as well as time synchronization. This repository contains the source code, documentation, unit tests, benchmarks as well as various examples of how to use the Nearest Advocate algorithm.
- GitHub-Repository: https://github.com/iot-salzburg/nearest-advocate
- Pip-Package: https://pypi.org/project/nearest-advocate/.
Install the package with:
pip install nearest_advocateOpen Python and import the required packages:
import numpy as np
import nearest_advocateCreate a reference and signal array of ordered timestamps: The reference array's inter-event intervals are sampled from a normal distribution. The signal array is a clone of the reference, shifted by np.pi and with Gaussian noise added. The event's timestamps of both arrays must be sorted!
arr_ref = np.sort(np.cumsum(np.random.normal(loc=1, scale=0.25, size=1000)))
arr_sig = np.sort(arr_ref + np.pi + np.random.normal(loc=0, scale=0.1, size=1000))The method nearest_advocate.nearest_advocate returns the two-columned array time_shifts with all investigated time-shifts (i.e., time-delays) and their respective mean distance of each signal timestamp to its nearest advocate event timestamp in the reference array. This is the algorithm's measure of the synchronicity between both arrays. A lower value indicates a higher synchronicity.
time_shifts = nearest_advocate.nearest_advocate(arr_ref=arr_ref, arr_sig=arr_sig, dist_max=0.25, td_min=-60, td_max=60)
time_shift, min_mean_dist = time_shifts[np.argmin(time_shifts[:,1])]
print(f"Estimated a time delay of {time_shift:.4f} s with a minimal mean distance of {min_mean_dist:.6f} s")
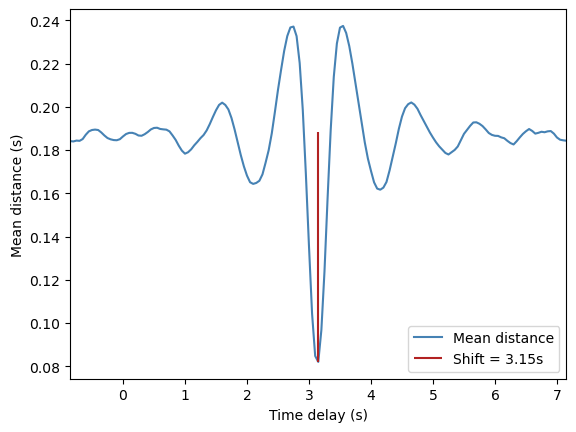
#> Estimated a time delay of 3.1469 s with a minimal mean distance of 0.077313 sThe time-delay of arr_sig is estimated to be approximately td_min and td_max as well as the adjustable resolution with the parameter samples-per-seconds sps.
Create a plot of the resulting characteristic curve of Nearest Advocate. The global minimum of this curve indicates the estimated time-delay of the signal array.
import matplotlib.pyplot as plt
plt.plot(time_shifts[:,0], time_shifts[:,1], color="steelblue", label="Mean distance")
plt.vlines(x=time_shift, ymin=min_mean_dist, ymax=np.mean(time_shifts[:,1]), color="firebrick", label=f"Time-Delay = {time_shift:.2f} s")
plt.xlim(time_shift-4, time_shift+4)
plt.xlabel("Time delay (s)")
plt.ylabel("Mean distance (s)")
plt.legend(loc="lower right")
plt.show()The characteristic curve in Figure indicates a prominent minimum at
The Nearest Advocate takes two arrays as input:
| Argument | Type | Description |
|---|---|---|
arr_ref |
list, array_like | Sorted reference array (1-D) with timestamps assumed to be correct. |
arr_sig |
list, array_like | Sorted signal array (1-D) of timestamps, assumed to be shifted by an unknown constant time-delta. |
The algorithm can be adjusted using following parameters:
| Parameter | Type | Description |
|---|---|---|
td_min |
float | Lower bound of the search space for the time-shift. |
td_max |
float | Upper bound of the search space for the time-shift. |
sps |
float, optional | Resolution or number of investigated time-shifts per second. Default None: sets it to 100 divided by the median gap of each array. |
dist_max |
float, optional | Maximal accepted distance between two advocate events; Default None set it to 1/4 of the smaller average gap between the array timestamps. |
sparse_factor |
int, optional | Factor for sparseness of arr_sig during calculation; higher is faster but less precise (default 1). |
symmetric |
bool, optional | Perform the Nearest Advocate algorithm symmetrically, i.e., twice with switched ref and probe signal, then averaging results from both array orders (default False). |
Examples on how to set the parameters for certain use-cases can be found in the following examples.
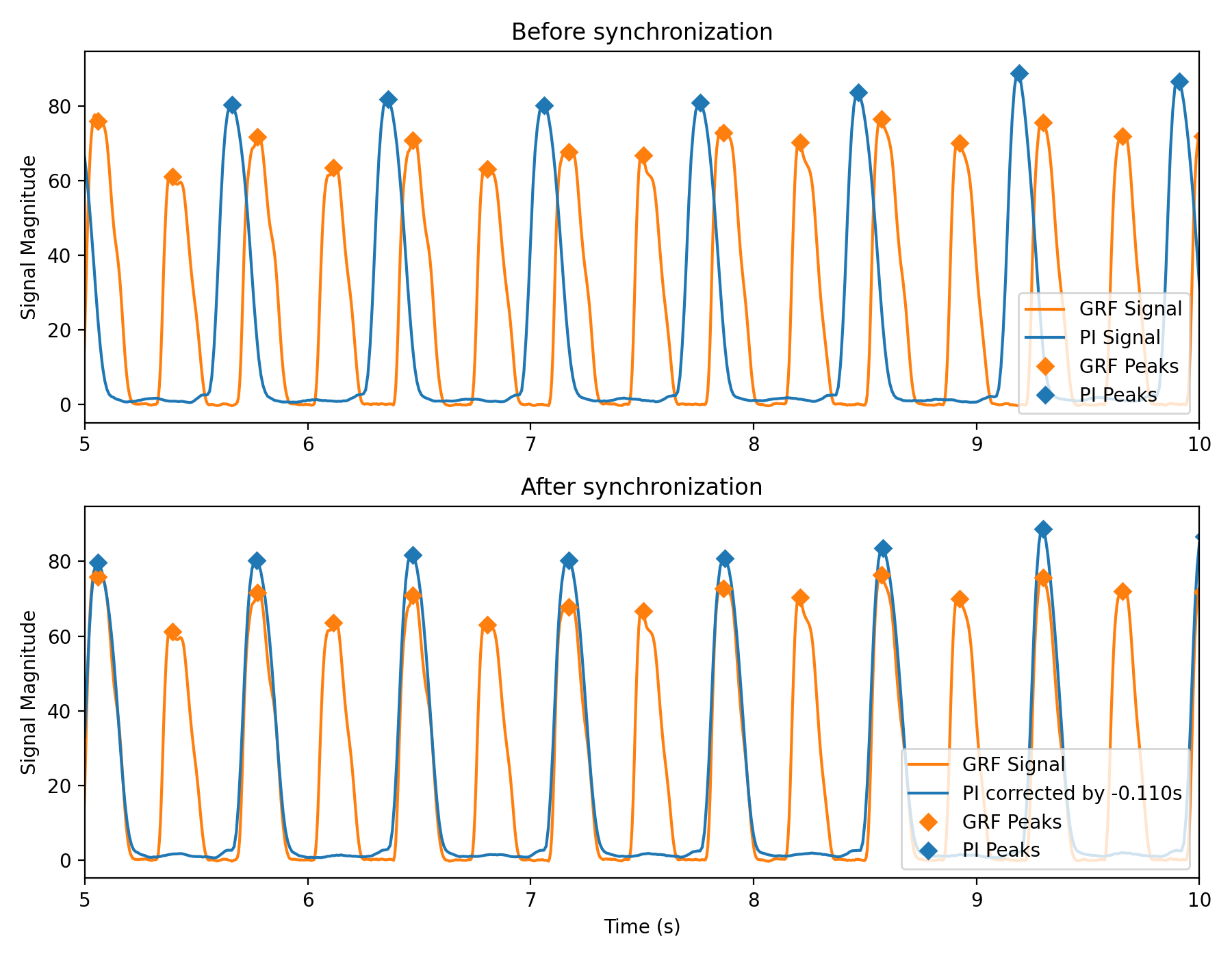
In human biomechanics, wearable measurements are regularly validated against a reference measurement (or gold standard). Thus, both measurements are acquired simultaneously and mostly with different controllers and different internal clocks. The subsequent evaluation of the wearable data requires a post-recording synchronization.
In the example, we have two measurements of a human running on a treadmill. The reference system is the treadmill, which measures the vertical forces of the feet on its belt (called reference signal). The probing signal is from wearable insoles that measure the pressure on the soles (called probing signal).
In biomechanics practice, often physical markers are executed at the start of recordings, such as jumps, which helps for the manual synchronization of the signal. In this example, we will show, that the time-series can be synchronized after recording even without such markers by using the Nearest Advocate Algorithm for Event-based Time-Delay Estimation.
A Jupyter notebook is provided to demonstrate the functionality and can be used as starting point for your own applications experiments/application_gait_measurements.ipynb. You will learn how to preprocess continuous signals to extract the event-timestamps (here from steps), such that they can be used as input for the NAd-algorithm.
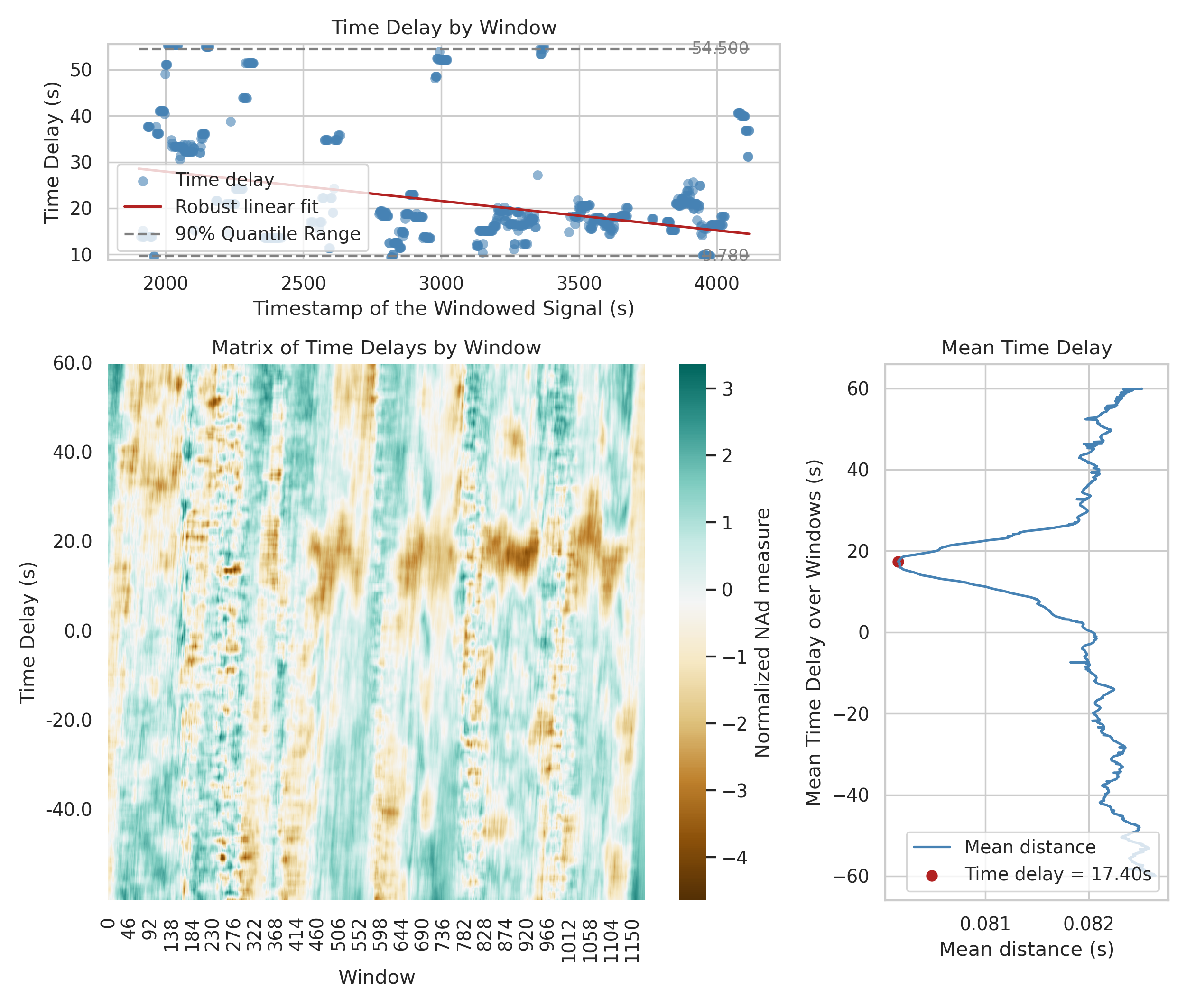
The most-common synchronization issue is a constant time-delay. This case is handled by the basic application of the Nearest Advocate algorithm. Using the NAd in sliding windows, it is possible to estimate a non-constant time-delay, i.e., a linear or non-linear trend, of the relative clock drift between two clocks. To do so, both event time-series should contain a higher number of timestamps.
A Jupyter notebook is provided for demonstration: experiments/application_nonlinear_correction.ipynb.
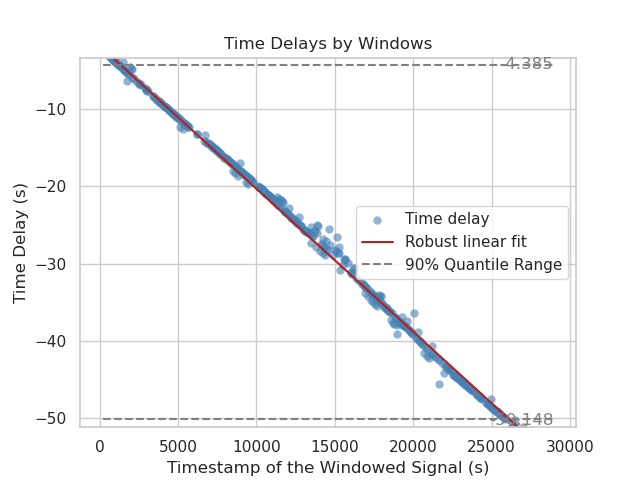
Example of a linear clock-drift correction:
Here the time-delay varies from around 0 s at the first part of the measurement to up to -50 s for the last parts with a clear linear trend.
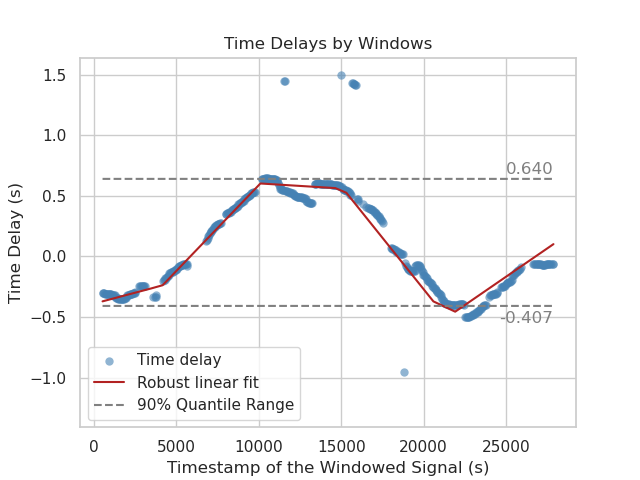
Example of a subsequent nonlinear clock-drift correction:
Here the time-delay varies from around -0.4 s to up to 0.64 s with a non-linear trend which is caused by a changing clock speed.
This algorithm is so robust against data quality issues, that it is even possible to estimate the time-delay between two event-based measurements of different observations. In experiments/application_different_observations.ipynb it is demonstrated how to apply the NAd for breathing and step events from the same participant and recording time. The breathing and steps are loosely coupled through the so-called locomotion-respiratory-coupling (LRC) which suffices to synchronize the recordings. However, the resulting accuracy has to be taken with a grain of salt.
Applied methods for windowed Nearest Advocate, linear and nonlinear clock-drift correction and advanced plotting is provided in experiments/nearest_advocate_windowed with sample Jupyter notebooks of how to use them in the parent directory.
As the main author and active user, I have already applied this algorithm for multiple use-cases from various domains. I even used it to determine the age of a house based on tree ring recordings.
Poorly synchronized measurements shouldn't be a limit anymore. Therefore, I challenge you to apply this method to your own data synchronization problems! I would be glad to hear from you what worked! In case you are not successful, need support, or doubt whether your data can be synchronized at all, feel free to contact me! I would be glad to help rescue your data.
I am open for sponsoring for companies or a co-authorship for universities! You can find contact information on my company's website.
When using in academic work, please cite:
Schranz, C., Mayr, S., Bernhart, S. et al. Nearest advocate: a novel event-based time delay estimation algorithm for multi-sensor time-series data synchronization. EURASIP J. Adv. Signal Process. 2024, 46 (2024). https://doi.org/10.1186/s13634-024-01143-1
or:
Schranz, C., & Mayr, S. (2022, September 29). Ein neuer Algorithmus zur Zeitsynchronisierung von Ereignis- basierten Zeitreihendaten als Alternative zur Kreuzkorrelation. Proceedings of the 14th Symposium of the Section Sport Informatics and Engineering of the German Society of Sport Science (dvs) (spinfortec2022), Chemnitz. https://doi.org/10.5281/zenodo.7370958