Leymosun: High-Entropy Randomness Research Toolkit

A package for randomness based research.

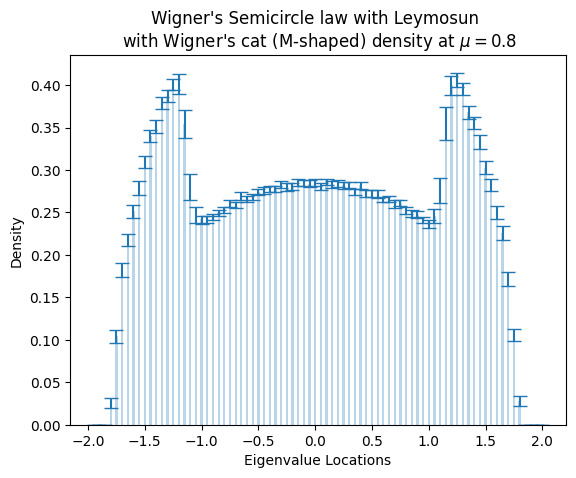
Figure Empirical spectral density for mixed ensemble at $\mu=0.8$, so called Wigner's Cats with error bars. (See the lecture.) This is also known as Wigner Cat Phases, see video. suzen25.

Installation

It is recommended that latest stable package is released on the Python Package Index (PyPI). PyPI version should be installed via pip.

pip install leymosun

It is recommended that package shouldn't be installed via github version control, unless it is a specific release.

Approach and features

The package provides tools and utilities for randomness based research with High-Entropy Random Number Generation (HE-RNG). It means generation is performed with non-deterministic seeds every time a random library function is called.

Having non-reproducible and unpredictable RNGs could improve Monte Carlo and similar randomness based computational science experimentation. Non-reproducible RNGs can still generate reproducible research. Critical components in this direction is Uncertainty Quantification (UQ). Leymosun implements bootstrapped based UQ and confidence interval generations.

High-entropy random number utilities

The core package is providing strong randomness improving the simulation quality. We use NumPy grammar and as a backend.

• HE-RNG random states.
• Distributions:
  • Bionomial
  • Uniform integer on the given range
  • Uniform float on the given range
  • Normal distribution (Gaussian)
  • Random sampling from a set, choice.

Random Matrices

• Generation of Gaussian ensembles (Orthogonal).
• Generation of Mixed Gaussian ensembles (Orthogonal) via Mixed Matrix Ensemble Sampling (MMES) algoritm
• Extract offdiagonal elements.
• Spectra generation given ensemble.
• Robust Spectral unfolding.
• Nearest-Neigbour Spacing Densities (NNSD).
• Adjacent gap ratio.
• Analytic distributions: Wigner semi-circle law, nearest-neigbour spacing.

Statistics

• Centered PDF computation.
• Bootstrapped uncertainty quantification given observation matrix.

Data manager

• Storage object utilities.

Lectures

Lectures notes that introduce randomization concepts with the usage of Leymosun.

• wigner_semicircle.ipynb: Lecture on the Wigner's semicircle law. The Wigner Semicircle law for the Gaussian Orthogonal Ensemble (GOE), comparison with the analytical case.
• wigner_dyson_spacing.ipynb: Lecture on the Wigner-Dyson nearest-neighbour distribution. The Wigner-Dyson spacing law for the Gaussian Orthogonal Ensemble (GOE), comparison with the analytical case.
• wigner_semicircle_mixed.ipynb: Lecture on the Wigner's cats. Deviations from the Wigner Semicircle law for the mixed-Gaussian Orthogonal Ensemble (GOE). This would demonstrate, so-called "Wigner's Cats", i.e., the deviation makes the density looks like cat.
• spectral_unfolding.ipynb: Self-consistent spectral unfolding understanding what is a spectral unfolding.
• he_rng_nist.ipynb: Lecture on Understanding High-Entropy RNGs with NIST benchmark. This lecture provides a way to test different RNGs or usage of RNGs via standard quality tests.

Development notes

• Philosophy
  There is a common misconception in computational sciences that speed is the ultimate goal, however primary objective is scientific correctness first. For this reasons, scientific correctness is taken precedence over speed in the development of the package. For proven methods being a baseline, we might implement faster versions.
• Testing
  • tests and nbconvert should be present as recommended dependency.
  • Test script should pass before any release. Unit tests runtests.sh and lectures runlectures.sh. (lecturePy directory is needed but this is ignored in the repo via .gitignore).
  • Add unit tests for each new method and features.
  • Add run portion for the new lecture in runlecture.sh.

Publications

Papers, datasets and other material that used leymosun.

• Empirical deviations of semicircle law in mixed-matrix ensembles, M. Suzen, HAL-Science, hal-03464130 (2021).
  2025 improvements with the leymosun package.

Citation

We would be grateful for a citation of our paper(s) if you use leymosun or ideas from the package in your research. Initial introduction of mixed matrix ensembles and MMES algorithm with M-shaped (Wigner's Cat) density [suzen21, suzen25]. The following is the bibtex entry

@article{suzen25,
  title={Wigner Cat Phases: A finely tunable system for exploring the transition to quantum chaos}, 
  author={S{\"u}zen, M.},
  year={2025},
  eprint={2512.22169},
  archivePrefix={arXiv},
  primaryClass={quant-ph},
  url={https://arxiv.org/abs/2512.22169}, 
}

@article{suzen21,
  title={Empirical deviations of semicircle law in mixed-matrix ensembles},
  author={S{\"u}zen, Mehmet},
  year={2021},
  journal={HAL-Science},
  url={https://hal.science/hal-03464130/}
}

License

(c) 2025
M. Süzen

All codes are released under GPLv3.
Documentations are released under CC BY 4.0.