设计一个类,只能生成该类的一个实例
单例模式需要满足如下规则:
- 构造函数私有化(private),使得不能直接通过new的方式创建实例对象;
- 通过new在代码内部创建一个(唯一)的实例对象;
- 定义一个public static的公有静态方法,返回上一步中创建的实例对象;由于在静态方法中,所以上一步的对象也应该是static的。
public class EagerSingleton {
//类加载时先New一个出来
private static EagerSingleton eagerSingleton = new EagerSingleton();
private EagerSingleton() {
}
public static EagerSingleton getInstance() {
return eagerSIngleton;
}
public static void main(String[] args) {
EagerSingleton s1 = EagerSingleton.getInstance();
EagerSingleton s2 = EagerSingleton.getInstance();
System.out.println(s1 == s2);
}
}public class LazySingleton {
private LazySingleton() {
}
private static LazySingleton instance = null;
public static LazySingleton getInstance() {
if (instance == null) {
//锁定代码块
synchronized (LazySingleton.class) {
//第二重判断
if (instance == null) {
instance = new LazySingleton();
}
}
}
return instance;
}
}package edu.xjtu.soto.chap2;
/**
* @author wst
* @create 2019-09-05 20:18
*/
public enum EnumSingleton {
INSTANCE;
}在一个长度为n的数组里的所有数字都在0~n-1的范围内,数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次,请找出数组中任意一个重复的数字.
例如:如果输入长度为7的数组{2,3,1,0,2,5,3}那么对应的输出是重复的数字2或者3
public Boolean duplicate1(int[] arrays,int length,int[] duplicate) {
if (arrays == null || arrays.length != length || length == 0 ) {
return false;
}
Arrays.sort(arrays);
for (int i = 0; i < arrays.length - 1; i++) {
if (arrays[i] == arrays[i + 1]) {
duplicate[0] = arrays[i];
return true;
}
}
return false;
}public Boolean duplicate2(int[] arrays, int length, int[] duplicate) {
if (arrays == null || arrays.length != length || length == 0 ) {
return false;
}
for (int i = 0; i < length; i++) {
if (arrays[i] < 0 || arrays[i] > length-1) {
return false;
}
}
for (int i = 0; i < length; i++) {
while (i != arrays[i]) {
if (arrays[arrays[i]] == arrays[i]) {
duplicate[0] = arrays[i];
return true;
}
swap(arrays, i, arrays[i]);
}
}
return false;
}- 长度为n的数组里包含一个或多个重复的数字
- 数组中不包含重复的数字
- 无效输入测试用例(输入空指针;长度为n的数组中包含0~n-1之外的数字)
在一个长度为n+1的数组里的所有数字都在1-n 的范围内,所以数组中至少有一个数字是重复的,请找出数组中任意一个重复的数字,但不能修改输入的数组。
例如:如果输入长度为8的数组{2,3,5,4,3,2,6,7},那么对应的输出重复数字为2或3
public int duplicate(int[] arrays, int length, int[] duplicate) {
if (arrays == null || arrays.length <= 0 || length != arrays.length) {
return 0;
}
for (int i = 1; i < length ; i++) {
if (arrays[i] < 1 || arrays[i] > length - 1) {
return 0;
}
}
for (int i = 1; i < length; i++) {
if (arrays[i] == duplicate[arrays[i]]) {
return arrays[i];
}
duplicate[arrays[i]] = arrays[i];
}
return 0;
}在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序,请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
例如下面的二维数组就是每行,每列都递增排序。如果在这个数组中查找数字7,则返回true;如果想找数字5,由于数组不含有该数字,则返回false
| 1 | 2 | 8 | 9 |
|---|---|---|---|
| 2 | 4 | 9 | 12 |
| 4 | 7 | 10 | 13 |
| 6 | 8 | 11 | 15 |
首先选取数组中右上角的数字,如果该数字等于要查找的数字,则查找过程结束;如果该数字大于要查找的数字,则剔除这个数字所在的列;如果该数字小于要查找的数字,则剔除为个数字所在的行。也就是说,如果要查找的数字不在数组的右上角,则每一次都在数组的查找范围中剔除一行或一列,这样每一步都可以缩小查找的范围,直到查找的数字,或者查找范围为空。
public boolean find2(int[][] arrays, int target) {
if (arrays == null || arrays.length <= 0) {
return false;
}
int row = 0;
int rows = arrays.length;
int cols = arrays[0].length-1;
while (row < rows && cols >= 0) {
if (arrays[row][cols] > target) {
cols--;
}else if (arrays[row][cols] <target) {
row++;
} else{
return true;
}
}
return false;
}- 二维数组中包含查找的数字(查找的数字是数组中的最大值和最小值;查找的数字介于数组中的最大值与最小值之间)
- 二维数组中没有查找的数字(查找的数字大于数组中的最大值;查找的数字小于数组中的最小值;查找的数字在数组的最大值和最小值之间但数组中没有这个数字)
- 特殊输入测试(输入空指针)
题目:请实现一个函数。把字符串中的每个空格替换成”%20“。例如,输入”We are happy“,则输出”We%20are%20happy“
public String replaceBlank1(StringBuffer s) {
if (s == null || s.length() == 0) {
return null;
}
return s.toString().replace(" ", "%20");
}从前往后扫描要移动那么多次,不妨反过来从后往前扫描试试。
- 先遍历一遍原字符串,统计空格字符的个数。
- 由于要将空格(一个字符)变成
%20(三个字符),所以需要将原字符串增长2 * 空格数 - 设置两个指针,一个指针oldP指向原字符串的末尾;另一个指针newP指向增长后的新字符串末尾。不断将oldP处的字符移动到newP处,然后两个指针都要左移;如果oldP处字符是空格,就在newP处设置三个字符:按顺序分别是
0、2、%,同样的两个指针相应的左移。
public String replaceBlank2(StringBuffer s) {
if (s == null || s.length() == 0) {
return null;
}
int spaceNum = 0;
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i)== ' ') {
spaceNum++;
}
}
int oldP = s.length() - 1;
s.setLength(s.length() + 2 * spaceNum);
int newP = s.length() - 1;
while (oldP >= 0 && oldP != newP) {
if (s.charAt(oldP) == ' ') {
s.setCharAt(newP--, '0');
s.setCharAt(newP--, '2');
s.setCharAt(newP--, '%');
} else {
s.setCharAt(newP--, s.charAt(oldP));
}
oldP--;
}
return s.toString();
}- 输入的字符串中包含空格(空格位于字符串的最前面;空格位于字符串的最后面,空格位于字符串的中间,字符串中有连续多个空格
- 输入的字符串中没有空格
- 特殊输入测试(字符串是一个nullptr指针;字符串是一个空字符串;字符串只有一个空格字符;字符串中有连续多个空格)
有两个有序的数组A1和A2,A1末尾有足够空间容纳A2。实现一个函数将A2的所有数字插入到A1中,并且所有数字是有序的。
因为空闲的空间在A1的末尾,所以从后往前比较两个A1和A2的数字,将更大的那个移动到A1的末尾,然后左移指针,继续比较两个数组中的数。当某个数组中的元素被取完了,就直接从另外一个数组取。
比如下面的例子
A1 = [1, 2 ,4 ,7, 9, , , ...]
A2 = [3, 5, 8, 10, 12]
假设A1的长度为10,现暂时只有5个元素,这个长度刚好能装下A2。从后往前比较A1和A2:12比9大,将12移动到A1[9]中,然后9和10继续比较,10移动到A1[8]中,9和8比较9移动到A1[7]中,如此这般直到扫描完两个数组,所有数字也都有序了。
public class MergeTwoSortedArray {
public static void merge(Integer[] a, Integer[] b) {
if (a.length < b.length) {
return;
}
int la = 0;
for (int i = 0; i < a.length; i++) {
if (a[i] != null) {
la++;
}
}
la--;
int k = la + b.length ;
int lb = b.length-1;
while (k >= 0 && lb>=0) {
if (b[lb] > a[la]) {
a[k--] = b[lb--];
} else if (b[lb] < a[la]) {
a[k--] = a[la--];
} else if (b[lb] == a[la]) {
a[k--] = a[la--];
lb--;
}
}
}
public static void main(String[] args) {
Integer[] a = new Integer[10];
for (int i = 0; i < 4; i++) {
a[i] = 2 * i + 1;
}
Integer[] b = {1, 4, 6, 8};
merge(a, b);
System.out.println(Arrays.toString(a));
}
}题目:输入一个链表的头节点,从尾到头反过来打印出每个节点的值。
链表定义如下
public class ListNode {
public int val;
public ListNode next = null;
public ListNode(int val) {
this.val = val;
}
}public static ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
if (listNode == null) {
return null;
}
LinkedList<Integer> stack = new LinkedList<>();
for (ListNode node = listNode; node != null; node = node.next) {
stack.push(node.val);
}
return new ArrayList<>(stack);
}public ArrayList<Integer> printListFromTailToHead2(ListNode listNode) {
if (listNode == null) {
return null;
}
printListFromTailToHead2(listNode.next);
arrayList.add(listNode.val);
return arrayList;
}- 功能测试(输入的链表有多个节点;输入的链表只有一个节点)
- 特殊输入测试(输入的链表头节点指针为nullptr)
题目:输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如,输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并输入它的头节点,二叉树和定义如下:
public class TreeNode {
public int val = 0;
public TreeNode left = null;
public TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
} public TreeNode reconstructBinaryTree(int[] preOrder, int[] inOrder) {
if (preOrder == null || inOrder == null || preOrder.length == 0 || inOrder.length == 0) {
return null;
}
return construct(preOrder,0,preOrder.length-1,inOrder, 0, inOrder.length-1);
}
private TreeNode construct(int[] preOrder, int startPre, int endPre, int[] intOrder, int startInOrder, int endInOrder) {
if (startPre > endPre || startInOrder > endInOrder) {
return null;
}
int rootValue = preOrder[startPre];
TreeNode root = new TreeNode(rootValue);
for (int i = 0; i < endInOrder; i++) {
if (intOrder[i] == rootValue) {
root.left = construct(preOrder, startPre + 1, startPre+i-startInOrder, intOrder, startInOrder, i - 1);
root.right = construct(preOrder, startPre + i-startInOrder+1, endPre, intOrder, i+1, endInOrder);
}
}
return root;题目:给定一棵二叉树和其中一个节点,如何找出中序遍历序列的下一节点?树中的节点除了有两个分别指向左,右节点的指针,还有一个指向父节点的指针。
public class TreeLinkNode {
public int val;
public TreeLinkNode left = null;
public TreeLinkNode right = null;
public TreeLinkNode next = null;
public TreeLinkNode(int val) {
this.val = val;
}
}要找出中序遍历的下一个结点,要分几种情况探讨。
- 如果当前结点的右子结点不为空,那么下一个结点就是以该右子结点为根的子树的最左子结点;
- 如果当前结点的右子结点为空,看它的父结点。此时分两种情况,如果父结点的右子结点就是当前结点,说明这个结点在中序遍历中已经被访问过了,需要继续往上看其父结点...直到父结点的左子结点是当前结点为止,该父结点就是下一个结点。如果在一直往上的过程中已经到达根结点,而根结点的父结点为null,这种情况说明当前结点已经是中序序列的最后一个结点了,不存在下一个结点,应该返回null.
public static TreeLinkNode getNextNode(TreeLinkNode target) {
if (target == null) {
return null;
}
if (target.right != null) {
target = target.right;
while (target.left != null) {
target = target.left;
}
return target;
}
if (target.right == null) {
if (target == target.next.left) {
return target.next;
} else {
target = target.next;
while (target.next != null && target != target.next.left ) {
target = target.next;
}
if (target.next == null) {
return null;
} else {
return target.next;
}
}
}
return null;
}- 普通二叉树(完全二叉树,不完全二叉树)
- 特殊二叉树(所有节点都没有右子节点的二叉树;所有节点都没有左子节点的二叉树;只有一个节点的二叉树;二叉树的根节点指针为null)
- 不同位置的节点的下一个节点(下一个节点为当前节点的右子节点,右子树的最左子节点,父节点,跨层的父节点等;当前节点没有下一个节点)
题目:队列的声明如下,请实现它的两个函数appendTail和deleteHead,分别完成在队列尾部插入节点和在队列头部删除节点的功能。
private LinkedList<Integer> stack1 = new LinkedList<>();
private LinkedList<Integer> stack2 = new LinkedList<>();
public void enqueue(int node) {
stack1.push(node);
}
public int dequeue() {
if (stack1.isEmpty() && stack2.isEmpty()) {
throw new RuntimeException("队列为空");
}
if (stack2.isEmpty()) {
while (!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
}
return stack2.pop();
}- 往空的队列里添加,删除元素
- 往非空的队列里添加,删除元素
- 连续删除元素直至队列为空
刚开始两个队列都为空,进栈时,可以进入任意一个队列。不妨默认进入Queue a。后续进栈时操作,哪个队列不为空(将看到,另外一个队列肯定为空)就进入该队列中。出栈操作,最后进入队列的要先出栈,而此时要出栈的元素在队列最后,但是队列只支持在队列头删除,因此将除了最后一个元素之外的所有元素都删除并复制一份到另一个队列Queue another,然后出列最后一个元素即可。此时Queue a成了空队列。之后每次出列操作都像上述以样:将不为空的队列中除最后一个元素的其余元素删除并复制到另一个空队列中,再删除原队列中唯一一个元素并弹出。每次出栈操作后,总有一个队列是空的。又因为进栈时也是进入不为空的那个队列,因此进出栈操作时总有一个队列是空的。
这两个队列不像上面的例子中有明确的分工,在两个队列实现栈的例子中,它们交替实现进栈或出栈的功能。
总结一下:
- 进栈,进入不为空的那个队列中
- 出栈,将不为空队列中除倒数最后一个元素外的其余元素移动到另一个空队列中,紧接着弹出原队列的最后一个元素。
public class TwoQueueImpStack {
private Queue<Integer> q1 = new LinkedList<>();
private Queue<Integer> q2 = new LinkedList<>();
public void push(int node) {
if (q1.isEmpty() && q2.isEmpty()) {
q1.offer(node);
} else if (!q1.isEmpty()) {
q1.offer(node);
} else {
q2.offer(node);
}
}
public int pop() {
if (q1.isEmpty() && q2.isEmpty()) {
throw new RuntimeException("栈已空");
}
if (!q1.isEmpty()) {
for (int i = 0; i < q1.size()-1; i++) {
q2.offer(q1.poll());
}
return q1.poll();
} else{
for (int i = 0; i < q2.size()-1; i++) {
q1.offer(q2.poll());
}
return q2.poll();
}
}
public static void main(String[] args) {
TwoQueueImpStack a = new TwoQueueImpStack();
a.push(54);
a.push(55);
a.push(56);
System.out.println(a.pop());
System.out.println(a.pop());
a.push(53);
System.out.println(a.pop());
a.push(52);
System.out.println(a.pop());
System.out.println(a.pop());
}
}写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项。斐波那契数列的定义如下: $$ f(n) = \begin{cases} 0 & \text{n=0} \ 1 & \text{n=1} \ f(n-1)+f(n-2) &\text{n>1} \end{cases} $$
public static long fibonacci(int n) {
if (n < 0) {
throw new RuntimeException("非法数字");
}
int[] result = {0, 1};
if (n < 2) {
return result[n];
}
long MinOne = 1;
long MinTwo = 0;
long fibN = 0;
for (int i = 2; i <= n; i++) {
fibN = MinOne + MinTwo;
MinTwo = MinOne;
MinOne = fibN;
}
return fibN;
}public static long finbonacci2(int n) {
if (n == 1 || n == 0) {
return n;
}
return finbonacci2(n - 1) + finbonacci2(n - 2);
}题目2: 一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶,求该青蛙跳上一个n级台阶总共有多少种跳法。
到达1级台阶只有1种可能,到达2级台阶有2种可能;可记为f(1) = 1,f(2) = 2。要到达3级台阶,可以选择在1级台阶处起跳,也可以选择在2级台阶处起跳,所以只需求到达1级台阶的可能情况 + 到达2级台阶的可能情况,即f(3) = f(2) +f(1)
同理到达n级台阶,可以在n-1级台阶起跳,也可在n-2级台阶起跳,f(n) = f(n-2)+f(n-1)
可以看做是斐波那契数列。
public static long fabonacci(long n) {
if (n == 1 || n == 2) {
return n;
}
if (n < 1) {
throw new RuntimeException("非法值");
}
long a = 1;
long b = 2;
long f = 0;
for (int i = 3; i <= n; i++) {
f = a + b;
a = b;
b = f;
}
return f;
}- 功能测试(输入3,5,10)
- 边界值测试(如输入0,1,2)
- 性能测试(输入较大的数字,如40,50,100等)
public static void quickSort(int[] array,int low,int high) {
int i = low;
int j = high;
if (low < high) {
int piv = array[low];
while (low < high) {
while (low<high && array[high] >= piv) {
high--;
}
if (low < high) {
array[low] = array[high];
low++;
}
while (low < high && array[low] < piv) {
low++;
}
if (low < high) {
array[high] = array[low];
high--;
}
}
array[low] = piv;
quickSort(array, i, low - 1);
quickSort(array, low + 1, j);
}
}题目:请实现一个排序算法,要求时间效率为O(n)
对公司所有员工的年龄排序,公司员工人数几万,可以使用辅助空间
public static void ageSort(int[] ages) {
if (ages == null) {
return;
}
int[] temp = new int[100];
for (int i = 0; i < ages.length; i++) {
temp[ages[i]]++;
}
int index = 0;
for (int i = 0; i < 100; i++) {
for (int j = 0; j < temp[i]; j++) {
ages[index++] = i;
}
}
}公司员工的年龄有一个范围,在上面的代码中,允许的范围是0-99岁。数组temp来统计每个年龄出现的次数,某个年龄出现了多少次,就在数组ages里设置几次该年龄,这就相当于组数组ages排序了。该方法用长度100的整数数组作为辅助空间换来了O(n)的时间效率。
题目:把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转。输出旋转数组的最小元素。例如,数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1
public class SpanArrayMin {
public static int spanArrayMin(int[] array) {
if (array == null || array.length == 0) {
throw new RuntimeException("非法输入");
}
int low = 0;
int high = array.length - 1;
if (array[low] < array[high]) {
return array[low];
}
while (low + 1 != high) {
int mid = (low + high) / 2;
if (array[mid] == array[low] && array[mid] == array[high]) {
return inorder(array, low, high);
}
if (array[mid] >= array[low]) {
low = mid;
}
if (array[mid] <= array[high]) {
high = mid;
}
}
return array[high];
}
private static int inorder(int[] array, int low, int high) {
int res = array[low];
for (int i = low; i < high; i++) {
if (array[i] < res) {
res = array[i];
}
}
return res;
}
public static void main(String[] args) {
int[] array1 = {3, 4, 5, 0, 2, 3};
int[] array2 = {1, 2, 3, 4, 5, 6};
int[] array3 = {1, 0, 1, 1, 1};
int[] array4 = {1, 1, 1, 0, 1};
int[] array5 = {1, 1, 1, 1, 1};
System.out.println(spanArrayMin(array1));
System.out.println(spanArrayMin(array2));
System.out.println(spanArrayMin(array3));
System.out.println(spanArrayMin(array4));
System.out.println(spanArrayMin(array5));
}
}- 功能测试(输入的数组是升序排序数组的一个旋转,数组中有重复数字或者没有重复数字)
- 边界值测试(输入的数组是一个升序排序的数组,只包含一个数字的数组)
- 特殊输入测试(输入null指针)
public class BubbleSort {
public static void bubbleSort(int[] array) {
boolean flag = true;
while (flag) {
flag = false;
for (int i = 1; i < array.length ; i++) {
if (array[i] < array[i - 1]) {
swap(array, i, i - 1);
flag = true;
}
}
}
}
private static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
public static void main(String[] args) {
int[] array = {49, 38, 65, 97, 76, 13, 27, 49};
bubbleSort(array);
System.out.println(Arrays.toString(array));
}
}题目:请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始,每一步可以在矩阵中向左,右,上,下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。例如,在下面的3x4的矩阵中包含一条字符串“bfce”的路径(路径中的字母用下划线标出)。但矩阵中不包含字符串“abfb”的路径,因为字符串的第一个字符b占据了矩阵中的每一行第二个格子之后,路径不能再次进入这个格子。
| a | b |
t | g |
|---|---|---|---|
| c | f |
c |
s |
| j | d | e |
h |
这有点像图的深度优先搜索。除了矩阵边界,每个点都可以在4个方向上选择任意一个前进。当某一条路径失败后,需要回溯到上一次选择处,选择另一个方向再尝试。如果该处的方向都被尝试过了,继续回溯到上次选择处...每一次选择都会来到一个新的格子,在这个格子处又有若干个方向可选择,就这样不断前进、回溯、再前进,直到找到一条满足要求的路径为止;如果所有点都作为起点搜索一遍后还是没有找到满足要求的路径,说明在这个矩阵中不存在该条路径。
上面的描述,使用递归比较好理解。还有一点需要注意,由于路径上访问过的点不能进入第二次,所以需要一个boolean[] marked标记那些当前路径上被访问过的点。
public class HasPath {
public static boolean hasPath(char[] matrix, char[] str, int rows, int cols) {
if (matrix == null || str == null || str.length == 0 || rows < 1 || cols < 1) {
return false;
}
boolean[] marked = new boolean[rows * cols];
int pathLength = 0;
for (int row = 0; row < rows; row++) {
for (int col = 0; col < cols; col++) {
if (hasPathCore(matrix, rows, cols, row, col, str, pathLength,marked)) {
return true;
}
}
}
return false;
}
private static boolean hasPathCore(char[] matrix, int rows, int cols, int row, int col, char[] str, int pathLength, boolean[] marked) {
int index = row * cols + col;
if (row < 0 || col < 0 || marked[index] || matrix[index] != str[pathLength] || col > cols || row > rows) {
return false;
}
//递归深度到了字符串尾
if (pathLength == str.length - 1) {
return true;
}
marked[index] = true;
if (hasPathCore(matrix, rows, cols, row-1, col, str, pathLength+1, marked) ||
hasPathCore(matrix, rows, cols, row+1, col, str, pathLength+1, marked) ||
hasPathCore(matrix, rows, cols, row, col-1, str, pathLength+1, marked) ||
hasPathCore(matrix, rows, cols, row, col+1, str, pathLength+1, marked)) {
return true;
}
// 对于搜索失败需要回溯的路径上的点,则要重新标记为“未访问”,方便另辟蹊径时能访问到
marked[index] = false;
return false;
}
public static void main(String[] args){
String m = "abtgcfcsjdeh";
char[] matrix = m.toCharArray();
char[] path1 = {'b', 'f','c','f', 'f', 'e'};
char[] path2 = {'a','b','f','d'};
boolean b1 = hasPath(matrix, path1, 3, 4);
boolean b2 = hasPath(matrix, path2, 3, 4);
System.out.println(b1 + "\n" + b2);
}
}递归方法 hasPathTo中有个参数len,它表示当前递归的深度。第一次调用传入0,之后在其基础上的每一次递归调用len都会加1,递归的深度也反映了当前路径上有几个字符匹配相等了。能绕过下面的if判断,说明当前字符匹配相等了。接下来判断递归深度是否到达字符串末尾,比如字符串abc,第一次调用hasPath(传入len为0,递归深度为0)绕过了第一个if,说明字符a已经匹配相等,再判断len == str.length - 1不通过;再次递归,此时深度为1,绕过了第一个if,说明字符b已经匹配相等,再判断len == str.length - 1不通过;再次递归,此时深度为2,绕过了第一个if,说明字符c已经匹配相等,所有字符匹配相等,因此再次判断len == str.length - 1通过,应该返回true.
还有注意:四个方向搜索不是同时发生的,当某一个方向搜索失败后,会退回来进行下一个方向的搜索,回溯法就体现在此。
当搜索失败时,别忘了marked[index] = false;,将搜索失败路径上点重新标记为“未访问”,以便回溯后选择其他方向继续前进时能再次访问到这些点。
- 功能测试(在多行多列的矩阵中存在或者不存在路径)
- 边界值测试(矩阵只有一行或者只有一列:矩阵和路径中的所有字母都是相同的)
- 特殊输入测试(输入null)
题目:地上有一个m行n列的方格。一个机器人从坐标(0,0)的格子开始移动,它每次可以向左 右、上、下、移动一格,但不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格(35,37),因为3+5+3+7=18。但它不能进入方格(35,38),因为3+5+3+8=19.请问庐机器人能够到达多少个格子?
此题和面试题12——矩阵中的路径有相似之处,依然是回溯法。每来到一个新的且满足条件的格子时,计数加1。除矩形的边界外,任意一个方格都有四个方向可以选择,选择任一方向后来到新的格子又可以选择四个方向,但是一个到达过的格子不能进入两次,因为这将导致对同一个格子的重复计数。也就是说,**一个格子一旦满足条件进入后,就被永久标记为“访问过”,一个满足条件的格子只能使计数值加1。**这是和面试题12有区别的地方(那个例子中是搜索路径,失败路径上的点要重新标记为“未访问”,因为另开辟的新路径需要探索这些点)。
这道题用通俗的话来讲就是:m行n列的所有方格中,有多少个满足行坐标和列坐标的数位之和小于等于门限值k的格子?
代码和面试题12长得有点像,但是两个问题是有明显区别的!
public class MovingCount {
public static int movingCount(int threshold, int rows, int cols) {
if (threshold < 0 || rows <= 0 || cols <= 0) {
return 0;
}
boolean marked[] = new boolean[rows * cols];
return movingCountCore(threshold, rows, cols, 0, 0, marked);
}
private static int movingCountCore(int threshold, int rows, int cols, int row, int col, boolean[] marked) {
int count = 0;
if (check(threshold, rows, cols, row, col, marked)) {
marked[row * cols + col] = true;
count = 1 + movingCountCore(threshold, rows, cols, row - 1, col, marked)
+ movingCountCore(threshold, rows, cols, row + 1, col, marked)
+ movingCountCore(threshold, rows, cols, row, col - 1, marked)
+ movingCountCore(threshold, rows, cols, row, col + 1, marked);
}
return count;
}
private static boolean check(int threshold, int rows, int cols, int row, int col, boolean[] marked) {
if (row >= 0 && row< rows && col>=0 && col<cols && getDigitSum(row) + getDigitSum(col) <= threshold
&& !marked[row*cols+col]) {
return true;
}
return false;
}
private static int getDigitSum(int num) {
int sum = 0;
while (num > 0) {
sum += num % 10;
num = num / 10;
}
return sum;
}
public static void main(String[] args) {
int count = movingCount(2, 3, 4);
System.out.println(count);
}
}- 功能测试(方格为多行多列;k为正数)
- 边界值测试(方格只有一行或者一列;k等于0)
- 特殊输入测试(k 为负数)
题目:给你一根长度为n的绳子,请把绳子剪成m段(m,n都是整数,n>1并且m>1),每段绳子的长度记为k[0],k[1]....,k[m]。请问k[0]xk[1]x...xk[m]可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2,3,3的三段,此时得到的最在乘积是18.
首先定义函数f(n)为把长度为n的绳子剪成若干段后各段长度乘积的最大值。在剪第一刀的时候,我们有n-1种可能的选择,也就是剪出来的第一段绳子的可能长度分别不1,2,...,n-1。因此,f(n) = max(f(i)xf(n-i)),其中0<i<n
public static int maxProductAfterCutting_solution(int length) {
if (length < 2) {
return 0;
}
if (length == 2) {
return 1;
}
if (length == 3) {
return 2;
}
int[] products = new int[length + 1];
//先存绳子的长度
products[0] = 0;
products[1] = 1;
products[2] = 2;
products[3] = 3;
int max;
for (int i = 4; i <= length; i++) {
max = 0;
for (int j = 1; j <= i/2; j++) {
int product = products[j] * products[i - j];
if (max < product) {
max = product;
}
products[i] = max;
}
}
max = products[length];
return max;
}如果我们按照如下的策略来剪绳子,则得到的各段绳子的长度的乘积将最大:当n>=5时,我们尽可能多地剪长度为3的绳子;当剩下的绳子长度为4时,把绳子剪成两段长度为2的绳子。为种思路对应的参考代码如下:
public static int maxProductAfterCutting_solution2(int length) {
if (length < 2) {
return 0;
}
if (length == 2) {
return 1;
}
if (length == 3) {
return 2;
}
//尽可能多地剪去长度为3的绳子段
int timesOf3 = length / 3;
//当绳子最后剩下的长度为4的时候,不能再剪长度为3的绳子段
//此时更好的方法是殷绳子剪成长度为2的两段,因为2x2>1x3
if (length - timesOf3 * 3 == 1) {
timesOf3--;
}
int timesOf2 = (length - timesOf3 * 3) / 2;
return (int)(Math.pow(3, timesOf3) * Math.pow(2, timesOf2));
}- 功能测试(绳子的初始长度大于5)
- 边界值测试(绳子的初始长度分别为0,1,2,3,4)
题目:请实现一个函数,输入一个整数,输出该数二进制表示中1的个数,例如,把9表示成二进制是1001,有2位是1.因此,如果输入9,则该函数输出2.
容易想到的思路:该数的各位不断和1相与,然后将该数右移1位,直到所有位都比较过。
错误代码:
public static int numberOf1(int num) {
int count = 0;
while (num != 0) {
if ((num & 1) == 1) {
count++;
}
num = num >> 1;
}
return count;
}注意!上面的代码是错误的!对于非负数来说没有问题,但是当传入负数的时候,由于>>是带符号的右移,对于负数来说高位会以1补位,n永远也不会等于9,因此会出现无限循环。
在Java中右移分两种,一种是上面那样带符号的右移,用>>表示,如果数是正数高位以0补位,如果是负数高位以1补位;还有就是无符号的右移,用>>>表示,不论正负数,统统高位以0补位。因此只需改动将上述程序的>>改成>>>即可通过。
正解代码
public static int numberOf1(int num) {
int count = 0;
while (num != 0) {
if ((num & 1) == 1) {
count++;
}
num = num >>> 1;
}
return count;
}上面的第一个程序之所以会出现无限循环,是因为我们改变了被输入的数本身。换个角度,我们不改变输入的数,而是通过改变一个变量,那么不管是输入正负数都能得到正确答案。
所以用一个1和输入数的每一位相与,然后将这个1不断左移。
public static int numberOf1Left(int num) {
int count = 0;
int flag = 1;
while (flag != 0) {
if ((num & flag) != 0) {
count++;
}
flag = flag << 1;
}
return count;
}在这个解法中,循环的次数等于整数二进制的位数,32位的整数需要循环32次。下面介绍一种算法,整数中有几个1就只需要循环几次
把一个整数减去1,再和原整数做与运算,会把该整数最右边的1变成0.那么一个整数的二进制表示中有多少个1,就可以进行多少次这样的操作。
public static int numberOf1Best(int num) {
int count = 0;
while (num != 0) {
num = (num - 1) & num;
count++;
}
return count;
}- 正数(包括边界值1,0x7FFFFFFF)
- 负数(包括边界值0x80000000,0xFFFFFFFF)
- 0
题目:用一条语句判断一个整数是不是2的整数次方。
一个整数如果是2的整数次方,那么它的二进制表示中有且只有一位是1,而其他所有位都是0.根据前面的分析,把这个整数减去1之后再和它自己做与运算,这个整数中唯一的1就会变成0
public static boolean powOf2(int n) {
return ((n - 1) & n) == 0;
}题目:输入两个整数m和n,计算需要改变m的二朝向表示中的多少位才能得到n。
比如10的二进制表示为1010,13的二进制表示为1101。需要改变1010中的3位才能得到1101。
我们可以分为两步解决这个问题:
第一步求这两个数的异或;
第二步统计异或结果中1的位数
public static int changeM2N(int m, int n) {
int a = m ^ n;
int count = 0;
while (a != 0) {
count++;
a = (a - 1) & a;
}
return count;
}题目:实现了函数double Power(double base,int exponent),求base的exponent次方。不得使用库函数,同时不需要考虑大数问题。
public static double power(double base, int exponent) {
if (base == 0) {
return 0;
}
double result = 1.0;
int positiveExponent = Math.abs(exponent);
for (int i = 0; i < positiveExponent; i++) {
result = result * base;
}
return exponent < 0 ? 1 / result : result;
}我们要求 $$ a^n $$ ,分n为奇数和偶数两种情况,如下
$$ a^n = a ^{n /2} \times a ^{n /2} $$ ,n为偶数
$$ a^n = a ^{(n-1) /2} \times a ^{(n-1) /2} \times a $$ ,n为奇数
假如要求 $$ 2^{32} $$ ,按照上面连乘的思路,需要进行31次乘法;采用上面的公式,只需要5次:先求平方,然后求四次方、八次方、十六次方,最后三十二次方。将时间复杂度降到了O(lg n)。
public static double power2(double base, int exponent) {
if (base == 0) {
return 0;
}
double result = 1.0;
int positiveExponent = Math.abs(exponent);
while (positiveExponent != 1) {
//判断是否为奇数
if ((positiveExponent & 1) == 1) {
result = result * base;
}
base = base * base;
//positiveExponent 除以2
positiveExponent = positiveExponent >> 1;
}
return exponent < 0 ? 1 / (result * base) : result * base;
}题目:输入数字n,按顺序打印出从1到最大的n位十进制数。比如输入3,则打印出1,2,3一直到最大的3位数999
这道题有陷阱,可能容易想到输入4就打印1
9999,输入5就打印199999...那我要是输入100呢?int型不能表示出来吧,甚至更大的值,即便是long型也不能表示出来。
这是一道大数问题,牵涉到大数问题我们可以将其转化为字符串表示。因为字符串任意长度都行。
本题要求按照递增顺序打印出1~最大的n位十进制数,所以字符串的长度定也应该是n。首先将长度为n的字符串中每个字符初始化为0,比如n = 3时,字符串一开始为000。我们要做的只有两步:
- 模拟数字那样在字符串上做加法;
- 将字符串表达的数字打印出来,为了可读性需要忽略不必要的0;
从第一步得知,需要经常改变字符串,我们知道Java中字符串是不可变对象,意味着每次对String的改变都会产生一个新的字符串对象,这将浪费大量空间,所以在下面的程序中将使用StringBuilder。根据这些描述,可写出如下代码。
package edu.xjtu.soto.chap17;
/**
* 从1至m位 所有的数
*/
public class PrintToMaxOfNDigits {
/**
* 使用字符串模拟数字加法
* @param n
*/
public static void printToMaxOfNDigits1(int n) {
if (n <= 0) {
return;
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < n; i++) {
sb.append(0);
}
while (stillIncrease(sb)) {
print(sb);
}
}
/**
* 判断sb是否还能增加1
* @param sb
* @return
*/
private static boolean stillIncrease(StringBuilder sb) {
int len = sb.length();
int token = 0;
for (int i = len - 1; i >= 0; i--) {
int sum = sb.charAt(i) - '0' + token;
if (i == len - 1) {
sum++;
}
if (sum == 10) {
if (i == 0) {
return false;
} else {
//进位
sb.setCharAt(i, '0');
token = 1;
}
} else {
//没有进位
sb.setCharAt(i, (char) (sum + '0'));
//自增完退出
return true;
}
}
return false;
}
private static void print(StringBuilder sb) {
int start = sb.length();
for (int i = 0; i < sb.length(); i++) {
if (sb.charAt(i) != '0') {
start = i;
break;
}
}
if (start < sb.length()) {
System.out.println(sb.substring(start));
}
}
public static void main(String[] args) {
StringBuilder sb = new StringBuilder("010");
// print(sb);
printToMaxOfNDigits1(1);
}
}stillIncrease方法会对当前数进行加1操作,该方法返回一个布尔值,用来表明当前数还能不能继续增长。比如n = 3时,当前数为999已经是最大了,不能再增长,此时如果调用该方法就应该返回false,因此跳出循环,不会打印1000(虽然不打印,但实际在该方法中字符串已经从"999"被更新到了“1000”)。当当前数可以继续增长时,会先对个位上的数进行自增操作,如果此时得到的sum < 10,说明不需向前进位,直接退出并返回;如果sum == 10,说明需要向前进位,需要将当前位设置为0,然后进位设置为1,在下一循环中,需要加到在前一位上,继续判断这一位上需不需要进位......直到某位上sum < 10循环才终止。
print方法,为了符合人的阅读习惯,比如"002"其实就是数字2,应保证从左到右第一个不为0的数前面的0不会被打印出来。
public class printFrom1ToMaxOfNDigitRecur {
public static void printFrom1ToMaxOfNDigitRecur(int n) {
if (n <= 0) {
return;
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < n; i++) {
sb.append("0");
}
printRecur(sb, n, -1);
}
private static void printRecur(StringBuilder sb, int len, int index) {
if (index == len - 1) {
print(sb);
return;
}
for (int i = 0; i < 10; i++) {
sb.setCharAt(index+1, (char) (i + '0'));
printRecur(sb,len,index+1);
}
}
private static void print(StringBuilder sb) {
int start = sb.length();
for (int i = 0; i < sb.length(); i++) {
if (sb.charAt(i) != '0') {
start = i;
break;
}
}
if (start < sb.length()) {
System.out.println(sb.substring(start));
}
}
public static void main(String[] args) {
printFrom1ToMaxOfNDigitRecur(2);
}
}题目:在O(1)时间内删除链表节点
给定单向链表的头指针和一个节点指针,定义一个函数在O(1)时间内删除该节点,链表节点与函数的定义如下:
public class ListNode {
public int val;
public ListNode next = null;
public ListNode(int val) {
this.val = val;
}
}public class DeleteNode {
public static void deleteNode(ListNode head, ListNode p) {
if (head == null || p == null) {
return;
}
//要删除的节点不是尾节点
if (p.next != null) {
ListNode pNext = p.next;
p.val = pNext.val;
p.next = pNext.next;
pNext = null;
//是尾节点也是头节点
} else if (head == p) {
head = head.next;
//仅是尾节点
} else {
ListNode first = head;
while (first.next != p) {
first = first.next;
}
first.next = null;
}
}
}题目:在一个排序的链表中,如何删除重复的节点?
例如,链表1->2->3->3->4->4->5 处理后为 1->2->5
注意重复的结点不保留:并不是将重复结点删除到只剩一个,而是重复结点的全部会被删除。所以链表1->2->3->3->4->4->5 处理后不是1->2->3->4->5。
public class DeleteDuplication {
/**
* 重新添加头结点
* @param head
*/
public static void deleteDuplicate(ListNode head) {
if (head == null || head.next == null) {
return;
}
ListNode first = new ListNode(head.val - 1);
first.next = head;
ListNode pre = first;
ListNode p = pre.next;
while (p != null && p.next != null) {
if (p.val != p.next.val) {
p = p.next;
pre = pre.next;
} else {
p = p.next;
while (p.val == p.next.val) {
p = p.next;
}
p = p.next;
pre.next = p;
}
}
head = first.next;
first = null;
}
public static void main(String[] args) {
ListNode node11 = new ListNode(1);
ListNode node21 = new ListNode(2);
ListNode node31 = new ListNode(3);
ListNode node32 = new ListNode(3);
ListNode node33 = new ListNode(3);
ListNode node41 = new ListNode(4);
ListNode node42 = new ListNode(4);
ListNode node51 = new ListNode(5);
node11.next = node21;
node21.next = node31;
node31.next = node32;
node32.next = node33;
node33.next = node41;
node41.next = node42;
node42.next = node51;
deleteDuplicate(node11);
while (node11 != null) {
System.out.println(node11.val);
node11 = node11.next;
}
}
}题目:请实现一个函数用来匹配包含.和*的正则表达式。模式中的字符.表示任意一个字符,而*表示它前面的字符可以出现任意次(含0次)。在本题中,匹配是指字符串的所有字符匹配整个模式。例如,字符串aaa与模式a.a和ab*ac*a匹配,但与aa.a和ab*a不匹配。
注意.就是一个字符,而*前面必须有一个字符(可以是.)才有意义,所以可以将x*看成一个整体,其中x表示任意字符。*在匹配时有两种情况,第二个字符是*或者不是。
-
第二个字符不是
*号。这种情况很简单,第二个字符要么是.要么是一个具体的字符。此时如果第一个字符匹配成功了,只需将模式和文本指针都前进一位。比如ab和ac以及ab和.b,分别对应着字符一样、模式字符为.的情况。第一个字符匹配失败了,直接就可以得出结论——匹配失败。 -
第二个字符是
*。有几种情况:1、
*匹配0次,比如a*ab和ab匹配,此时需要将模式指针前移2位,文本指针保持不动;2、
*匹配了1次,比如a*b和ab匹配,此时需要将模式指针前移2位,文本指针前移1位;3、
*匹配了多次,比如a*b和aaab匹配,此时需要将模式保持不动,文本指针前移1位;同样的比较第二个字符的前提是第一个字符已经匹配成功。
我们将长度任意的模式和文本分解成一个或者两个字符,可以用递归地方法写出如下程序:
public class Match {
public static boolean match(char[] str, char[] pattern) {
if (str == null || pattern == null) {
return false;
}
return matchCore(str, pattern, 0, 0);
}
private static boolean matchCore(char[] str, char[] pattern, int s, int p) {
if (s == str.length && p == pattern.length) {
return true;
}
//模式串到头 ,文本串未到头 匹配失败
if (p == pattern.length && s < str.length) {
return false;
}
// 两种情况,1、模式和文本都没有到结尾
// 2、或者文本到了结尾而模式还没有到结尾,此时肯定会调用else分支
// 第二个字符是*
if (p < pattern.length - 1 && pattern[p + 1] == '*') {
if (s < str.length && str[s] == pattern[p] || (pattern[p] == '.' && s < str.length)) {
return matchCore(str, pattern, s, p + 2) ||
matchCore(str, pattern, s + 1, p + 2) ||
matchCore(str, pattern, s + 1, p);
}else {
return matchCore(str, pattern, s, p + 2);
}
}
//第二个字符不是*
if ((s < str.length && str[s] == pattern[p]) || (pattern[p] == '.' && s < str.length)) {
return matchCore(str, pattern, s + 1, p + 1);
}
return false;
}
public static void main(String[] args) {
boolean b = match("aaa".toCharArray(), "a.a".toCharArray());
System.out.println(b);
}
}如果匹配的最后两个指针都到达末尾,说明完全匹配上了,返回true。如果模式指针先于文本到达末尾,一定是匹配失败了,举个例子,a*bcd和abcdefg。
接下来的两个if分别是第二个字符为*和不为*的情况。
- 第二个字符为
*。在保证第一个字符已经匹配上的情况下,*可以有三种匹配方式,有任一种方式匹配成功即可,所以return语句中用的是||。 - 第二个字符不为
*。当第一个字符已经匹配上的情况下,直接将模式和文本的指针前移一位,即比较下一个字符。
如果不是上面的情况(比如第一个字符就匹配失败了),返回false。
题目:请实现一个函数用来判断字符串是否表示数值(包括整数和小数),例如,字符串“+100”,“5e2”,“-123”,“3.1416”及“-1E-16”都表示数值,但"12e","1a3.14",“1.2.3”,“+-5”及“12e+5.4”都不是。
/**
* 正则表达式匹配
* @param str
* @return
*/
public static boolean isNumeric(String str) {
if (str == null) {
return false;
}
return str.matches("[\\+\\-]?[0-9]*(\\.[0-9]+)?([Ee][\\+\\-]?[0-9]+)?");
}题目:输入一全整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。
public static void recorderOddEven(int[] array) {
if (array == null || array.length == 0) {
return;
}
int start = 0;
int end = array.length - 1;
while (start < end) {
while ((array[start] & 1) == 1) {
start++;
}
while ((array[end] & 1) == 0) {
end--;
}
if (start < end) {
int temp = array[start];
array[start] = array[end];
array[end] = temp;
}
}
}题目:输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。
例如,一个链表有6个节点,从头节点开始,它们的值依次是1、2、3、4、5、6。这个链表的倒数第3个节点是值为4的节点。链表节点定义如下:
public class ListNode {
public int val;
public ListNode next = null;
public ListNode(int val) {
this.val = val;
}
}public class FindKthToTail {
public static ListNode findKthToTail(ListNode head, int k) {
if (head == null || k == 0) {
return null;
}
ListNode p = head;
ListNode q = head;
for (int i = 0; i < k-1; i++) {
if (p.next != null) {
p = p.next;
} else {
return null;
}
}
while (p.next != null) {
q = q.next;
p = p.next;
}
return q;
}
public static void main(String[] args) {
ListNode head = new ListNode(1);
ListNode head2 = new ListNode(2);
ListNode head3 = new ListNode(3);
ListNode head4 = new ListNode(4);
ListNode head5 = new ListNode(5);
head.next = head2;
head2.next = head3;
head3.next = head4;
head4.next = head5;
System.out.println(findKthToTail(head, 6).val);
}
}- 功能测试(第k个节点在链表的中间;第k个节点是链表的头节点;第k个节曙中链表的尾节点)
- 特殊输入测试(链表头节点为null指针;链表的节点总数少于k;k等于0)
题目:如果一个链表中包含环,如何找出环的入口节点?
public static ListNode meetingNode1(ListNode head) {
if (head == null || head.next == null || head.next.next == null) {
return null;
}
ListNode p = head.next;
ListNode q = head.next.next;
while (p != q && q != null) {
p = p.next;
q = q.next.next;
}
if (q == null) {
return null;
} else {
q = head;
}
while (p != q) {
p = p.next;
q = q.next;
}
return p;
}- p走一步,q走2步,直至二者相遇
- 将q重置为头结点
- p q 各走一步,直至相遇,该点即为环
我们知道Set中不能存放相同的元素。当在遍历链表的过程中,不断将当前结点放入Set中,当第一次add失败时,说明这个结点之前已经访问过了,这个结点刚好就是环的入口结点。
/**
* 利用set的无序性
* @param head
* @return
*/
public static ListNode meetingNode2(ListNode head) {
if (head == null || head.next == null || head.next.next == null) {
return null;
}
ListNode p = head;
Set<ListNode> set = new HashSet<>();
while (set.add(p)) {
p = p.next;
}
return p;
}
public static void main(String[] args) {
ListNode l1 = new ListNode(1);
ListNode l2 = new ListNode(2);
ListNode l3 = new ListNode(3);
ListNode l4 = new ListNode(4);
ListNode l5 = new ListNode(5);
ListNode l6 = new ListNode(6);
l1.next = l2;
l2.next = l3;
l3.next = l4;
l4.next = l5;
l5.next = l6;
l6.next = l3;
ListNode result = meetingNode1(l2);
System.out.println(result == null ? -1 : result.val);
ListNode res = meetingNode2(l1);
System.out.println(res == null ? -1 : res.val);
}- 功能测试(链表中包含或者不包含环;链表中有多个或者只有一个节点)
- 特殊输入测试(链表头节点为null)
题目:定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。链表节点定义如下:
public class ListNode {
public int val;
public ListNode next = null;
public ListNode(int val) {
this.val = val;
}
}public static ListNode reverseList1(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode first = new ListNode(-1);
first.next = head;
ListNode p = head.next;
head.next = null;
ListNode q = p;
while (p != null) {
q = p.next;
p.next = first.next;
first.next = p;
p = q;
}
head = first.next;
first = null;
return head;
} /**
* 使用递归
* @param head
* @return
*/
public static ListNode reverseList2(ListNode head) {
if (head == null || head.next == null) {
return head;
}
//递归后的头节点
ListNode headNode = reverseList2(head.next);
head.next.next = head;
head.next = null;
return headNode;
}只可意会,不可言传
- 功能测试(输入的链表含有多个节点:链表中只有一个节点)。
- 特殊输入测试(链表头节点为null)
题目:输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍是递增排序的。
例如,输入链表1:1--3--5--7 链表2:2--4--6--8
合并之: 链表3 : 1--2--3--4--5--6--7--8
链表节点定义如下
public class ListNode {
public int val;
public ListNode next = null;
public ListNode(int val) {
this.val = val;
}
}public static ListNode merge(ListNode l1, ListNode l2) {
if (l1 == null) {
return l2;
}
if (l2 == null) {
return l1;
}
ListNode head= null;
ListNode p = l1;
ListNode q = l2;
if (l1.val <= l2.val) {
head = l1;
p = l1.next;
} else {
head = l2;
q = l2.next;
}
ListNode cur = head;
while (p != null || q != null) {
if (p == null) {
cur.next = q;
break;
} else if (q == null) {
cur.next = p;
break;
} else if (p.val < q.val) {
cur.next = p;
cur = cur.next;
p = p.next;
} else {
cur.next = q;
cur = cur.next;
q = q.next;
}
}
return head;
}- 功能测试(输入的两个链表有多个节点;节点的值互不相同或者存在值相等的多个节点)。
- 特殊输入测试(两个链表的一个或者两个头节点为null;两个链表中只有一个节点)。
题目:输入两棵二叉树A和B,判断B是不是A的子结构。二叉树节点的定义如下:
public class TreeNode {
public int val = 0;
public TreeNode left = null;
public TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}二叉树这种递归的数据结构。想到用递归的方法解决是很自然的。
首先我们要在二树A中找到和树B根结点值一样的结点R,结点R可能有多个,因为树A中的结点值可能不止一个与树B的根结点值相同。对于每个结点R,其子树都有可能是树A的子结构,因此只要还未在树A中找到一个子结构,就要继续遍历树A判断其他R结点。
对于某一个R结点,我们要求根结点R的左子结点、右子结点和树B根结点的左子结点、右子结点分别相等(值相等),而且R的子结点的左右子结点也要和B的子结点值相等......直到和树B的叶子结点也相等才说树A包含树B。这是个递归的过程。
对于这两个步骤,可写出如下
public class HasSubtree {
public static boolean hasSubtree(TreeNode root, TreeNode subRoor) {
boolean result = false;
if (root != null && subRoor != null) {
if (root.val == subRoor.val) {
result = doesTree1HasTree2(root, subRoor);
}
if (!result) {
result = hasSubtree(root.left, subRoor);
}
if (!result) {
result = hasSubtree(root.right, subRoor);
}
}
return result;
}
private static boolean doesTree1HasTree2(TreeNode t1, TreeNode t2) {
if (t2 == null) {
return true;
}
if (t1 == null) {
return false;
}
if (t1.val != t2.val) {
return false;
}
return doesTree1HasTree2(t1.left, t2.left)
&& doesTree1HasTree2(t1.right, t2.right);
}
public static void main(String[] args) {
TreeNode root1 = new TreeNode(1);
TreeNode root2 = new TreeNode(2);
TreeNode root3 = new TreeNode(3);
TreeNode root4 = new TreeNode(4);
TreeNode root5 = new TreeNode(5);
root1.left = root2;
root1.right = root3;
root2.left = root4;
root2.right = root5;
boolean b = hasSubtree(root2, root5);
System.out.println(b);
}
}- 功能测试(树A和树B都是普通的二叉树;树B是或者不是树A的子结构)
- 特殊输入测试(两棵二叉树的一个或者两全根节点为null;二叉树的所有节点都没有左子树或者右子树)
题目:请完成一个函数,输入一棵二叉树,该函数输出它的镜像。
二叉树节点的定义如下:
public class TreeNode {
public int val = 0;
public TreeNode left = null;
public TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}/**
* 递归求镜像(先序遍历)
* @param root
* @return
*/
public static TreeNode treeMirror1(TreeNode root) {
if (root == null || (root.left == null && root.right == null)) {
return root;
}
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
if (root.left != null) {
treeMirror1(root.left);
}
if (root.right != null) {
treeMirror1(root.right);
}
return root;
} /**
* 非递归,层次遍历
* @param root
*/
public static void treeMirror2(TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
if (node.left != null || node.right != null) {
TreeNode temp = node.left;
node.left = node.right;
node.right = temp;
}
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}/**
* 非递归前序遍历
* @param root
*/
public static void treeMirror3(TreeNode root) {
LinkedList<TreeNode> stack = new LinkedList<>();
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
if (root.left != null || root.right != null) {
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
}
root = root.left;
}
if (!stack.isEmpty()) {
root = stack.pop();
root = root.right;
}
}
}前序遍历是深度优先搜索,所以用到了栈;而层序遍历是广度优先搜索,用到队列。
前序遍历是只要某结点还有左子结点,就不断压入栈中,直到没有左子结点时弹栈,接着将根结点指向右子树重复上述过程。
层序遍历很简单,先将根结点入列,然后弹出根结点将根结点子结点入列,不断重复上述过程直到队列为空。
- 功能测试(普通二叉树;对叉树的所有节点都没有左子树或者右子树;只有一个节点的二叉树)。
- 特殊国俾测试(二叉树的根节点为null)
题目:请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
/**
* 使用递归
* @param root
* @return
*/
public static boolean isSymmetrical(TreeNode root) {
return isSymmetrical(root, root);
}
private static boolean isSymmetrical(TreeNode root1, TreeNode root2) {
if (root1 == null && root2 == null) {
return true;
}
if (root1 == null || root2 == null) {
return false;
}
if (root1.val != root2.val) {
return false;
}
return isSymmetrical(root1.left, root2.right)
&& isSymmetrical(root1.right, root2.left);
}如果遇到两棵子树都为空则返回true,这句代码隐含了**“空树也是对称的”**这样的信息。否则,只有一子树为空另一不为空,显然不是对称的;如果两个子树都不为空,比较它俩根结点的值,不相同肯定不是对称的。之后递归地对树的子树进行上述判断,直到检查到叶子结点,如果都满足就返回true。
思路和上面一样,非递归实现需要用到两个队列。队列A专门存入左子树,队列B专门存入右子树。
入列时,将左子树的左子结点和右子树的右子结点分别存入队列A和队列B,紧接着还要将左子树的右子结点和右子树的左子结点分别存入队列A和队列B。
出列时,两个队列同时出列一个元素,根据存入的顺序,这两个出列元素就是左子树的左子结点和右子树的右子结点,或者左子树的右子结点和右子树的左子结点。之后对这两个元素进行比较,比较操作和上面递归版本的一样。
/**
* 使用队列
* @param root
* @return
*/
public static boolean isSymmetrical2(TreeNode root) {
if (root == null) {
return true;
}
Queue<TreeNode> queue1 = new LinkedList<>();
Queue<TreeNode> queue2 = new LinkedList<>();
queue1.offer(root.left);
queue2.offer(root.right);
TreeNode p = null;
TreeNode q = null;
while (!queue1.isEmpty() && !queue2.isEmpty()) {
p = queue1.poll();
q = queue2.poll();
if (p == null && q == null) {
continue;
} else if (p == null || q == null) {
return false;
}
if (p.val != q.val) {
return false;
}
queue1.offer(p.left);
queue2.offer(q.right);
queue1.offer(p.right);
queue2.offer(q.left);
}
return true;
}- 功能测试(对称的二叉树:因结构而不对称的二 叉树;经霜你对称但节点的值不对称的二叉树)。
- 特殊输入测试(二叉树和根节点为null;只有一个节点的二叉树;所有节点的值都相同的二叉树),
题目:输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
例如,输入如下矩阵:
| 1 | 2 | 3 | 4 |
|---|---|---|---|
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 |
依次打印出数字:1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10
假设这个矩阵的行数是rows,列数是columns。打印第一圈的左上角的坐标是(0,0),第二圈的左上角的坐标是(1,1)。以此类推,我们注意到,左上角的坐标中行标和列标总是相同的,于是可以在矩阵中选取左上角为(start,start)的一圈作为我们分析的目标。
对于一个5x5的矩阵而言,最后一圈只有一个数字,对应的坐标为(2,2)。我们发现5>2x2。对于一个6x6的矩阵而言,最后一圈有4个数字,其左上角的坐标仍然为(2,2).我们发现6>2x2依然顾立,于是可以得出,让循环继续的条件是columns> startX x2 并且rows>startYx3。所以我们可以用如下的循环来打针矩阵:
public void printMatrixClockwisely(int[] numbers, int columns, int rows) {
if (numbers == null || columns <= 0 || rows <= 0) {
return;
}
int start = 0;
while (columns > start * 2 && rows > start * 2) {
PrintMatrixInCircle(numbers, columns, rows, start);
++start;
}
}我们把打印一圈分4步:
- 从左到右打印一行
- 从上到下打印一列
- 从右到左打印一行
- 从下到上打印一列
每一步我们根据起始坐标和终止坐标用一个循环就能打印出一行或者一列。
不过需要注意的是,最后一圈有可能退化成只有一行。只有一列,甚至只有一个数字,因此打针这样的一圈就不再需要4步。
因此,我们需要仔细分析打印每一步的前提条件,第一步总是需要的,因为打针一圈至少有一步。如果只有一行,那就不用第二步了。也就是需要第二步的前提条件是终止行号大于起始行号,需要第三步打印的前提条件是圈内至少有两行两列,也就是说除了要求终止行号大于起始行号,还要求终止列号大于起始列号。同理,需要打针第四步的前提条件是至少有三行两列,因此要求终止行号比起始行号至少大2,同时终止列号大于起始列号。
public class PrintMatrix {
private ArrayList<Integer> list = new ArrayList<>();
public void printMatrixClockwisely(int[][] numbers, int columns, int rows) {
if (numbers == null || columns <= 0 || rows <= 0) {
return;
}
int start = 0;
while (columns > start * 2 && rows > start * 2) {
PrintMatrixInCircle(numbers, columns, rows, start);
++start;
}
}
private void PrintMatrixInCircle(int[][] numbers, int columns, int rows, int start) {
int endX = columns - 1 - start;
int endY = rows - 1 - start;
//从左到右打印一行
for (int i = start; i <= endX; i++) {
int number = numbers[start][i];
list.add(number);
}
//从上到下打印一列
if (start < endY) {
for (int i = start+1; i <= endY ; i++) {
int number = numbers[i][endX];
list.add(number);
}
}
//从历到左打印一行
if (start < endX && start < endY) {
for (int i = endX - 1; i >= start; i--) {
int number = numbers[endY][i];
list.add(number);
}
}
//从下到上打印一列
if (start < endX && start < endY - 1) {
for (int i = endY - 1; i >= start + 1; i--) {
int number = numbers[i][start];
list.add(number);
}
}
}
public static void main(String[] args) {
PrintMatrix pm = new PrintMatrix();
int[][] numbers1 = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}, {13, 14, 15, 16}};
int[][] numbers2 = {{1, 2, 3, 4, 5}, {6, 7, 8, 9, 10}, {11, 12, 13, 14, 15}, {16, 17, 18, 19, 20}, {21, 22, 23, 24, 25}};
pm.printMatrixClockwisely(numbers1, 4, 4);
System.out.println(pm.list);
pm.list.clear();
pm.printMatrixClockwisely(numbers2, 5, 5);
System.out.println(pm.list);
}
}数组中有多行多列;数组中只有一行;数组中只有一列;数组中只有一行一列
题目:定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的min函数,在该栈中,调用min,push,及pop的时间复杂度都是O(1)。
有些很容易想到的方法:比如每次想获得栈中的最小元素,将栈中所有元素复制到另一个数据结构中(比如List),然后对这个列表排序可以很简单地得到最小值。但时间复杂度肯定就不是O(1)了。
或者设置一个全局变量min,每次push都和当前最小值比较,如果更小就更新min,否则min不变。但是这种方法有个问题:要是pop出栈的元素正好就是这个min呢,那新的min是多少?我们很难得知,所以另辟蹊径。考虑到要求我们用O(1)的时间复杂度。可以考虑用空间换时间,试试使用辅助空间。
定义一个栈stackMin,专门用于存放当前最小值。
- 存放数据的stack存入当前元素,如果即将要存入的元素比当前最小元素还小,stackMin存入这个新的最小元素;否则,stackMin将当前最小元素再次存入。
- stack出栈时,stackMin也出栈。
反正就是入栈时,两个栈都有元素入栈;出栈时,两个栈都弹出一个元素。这两个栈总是同步进出栈的
public class StackIncludeFuncMin {
private LinkedList<Integer> stack = new LinkedList<>();
//辅助栈,用于存储当前最小值
private LinkedList<Integer> stackMin = new LinkedList<>();
public void push(int node) {
stack.push(node);
if (stackMin.isEmpty() || node < stackMin.peek()) {
stackMin.push(node);
} else {
stackMin.push(stackMin.peek());
}
}
public void pop() {
if (stack.isEmpty()) {
throw new RuntimeException("stake is empty!");
}
stack.pop();
stackMin.pop();
}
public int top() {
if (stack.isEmpty()) {
throw new RuntimeException("stack is empty!");
}
return stack.peek();
}
public int min() {
if (stackMin.isEmpty()) {
throw new RuntimeException("stack is empty!");
}
return stackMin.peek();
}
public static void main(String[] args) {
StackIncludeFuncMin stackIncludeFuncMin = new StackIncludeFuncMin();
stackIncludeFuncMin.push(5);
System.out.println(stackIncludeFuncMin.min());
stackIncludeFuncMin.push(4);
System.out.println(stackIncludeFuncMin.min());
stackIncludeFuncMin.push(6);
System.out.println(stackIncludeFuncMin.min());
stackIncludeFuncMin.push(3);
System.out.println(stackIncludeFuncMin.min());
stackIncludeFuncMin.pop();
System.out.println(stackIncludeFuncMin.min());
stackIncludeFuncMin.pop();
System.out.println(stackIncludeFuncMin.min());
stackIncludeFuncMin.pop();
System.out.println(stackIncludeFuncMin.min());
}
}我们来模拟一下:
| 出入栈 | stack | stackMin | min |
|---|---|---|---|
| 压入5 | 5 | 5 | 5 |
| 压入4 | 5, 4 | 5, 4 | 4 |
| 压入6 | 5, 4, 6 | 5, 4, 4 | 4 |
| 压入3 | 5,4,6,3 | 5, 4, 4, 3 | 3 |
| 弹出 | 5,4,6 | 5, 4, 4 | 4 |
| 弹出 | 5, 4 | 5, 4 | 4 |
| 弹出 | 5 | 5 | 5 |
举点例子模拟能很好地帮助我们理解。
- 新压入栈的数字比之前的最小值大
- 新压入栈的数字比之前最小值小
- 弹出栈的数字不是最小元素
- 弹出栈的数字是最小元素
题目:输入两个整数序列。第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。 例如,序列{1,2,3,4,5,}是某栈的压栈序列,序列{4,5,3,2,1}是该压栈序列对应的一个弹出序列,但{4,3,5,1,2}就不可能是该压栈序列的弹出序列。
题目只是给出了两个序列,并没有栈,所有我们需要自己定义一个辅助栈帮助我们模拟入栈出栈过程。
需要用到一个指针表示在出栈序列中的当前出栈元素。每次入栈一个元素,之后立刻和出栈序列中当前出栈元素对比,若相同就弹出刚压入的元素、同时当前弹出元素指针前移。之后还要继续比较,如果栈顶还和当前弹出元素相同则需要接着弹出。否则压入入栈序列中的下一个元素。
正常情况下,如果出栈顺序正确,当入栈序列中的元素都被压入后,辅助栈能按照出栈序列全部弹出。如果当元素都被压入后,辅助栈没能弹出所有元素(不为空),说明出栈顺序是错误的。
/**
*
* @param push 压入序列
* @param pop 弹出序列
* @return
*/
public boolean isPopOrder(int[] push, int[] pop) {
if (push == null || pop == null || push.length == 0 || pop.length == 0) {
return false;
}
int position = 0;
LinkedList<Integer> stackAur = new LinkedList<>();
for (int i = 0; i < push.length; i++) {
stackAur.push(push[i]);
while (!stackAur.isEmpty() && stackAur.peek() == pop[position]) {
stackAur.pop();
position++;
}
}
return stackAur.isEmpty();
}
public static void main(String[] args) {
int[] push = {1, 2, 3, 4, 5};
int[] pop1 = {4, 5, 3, 2, 1};
int[] pop2 = {4, 3, 5, 1, 2};
StackPopOrder stackPopOrder = new StackPopOrder();
boolean b1 = stackPopOrder.isPopOrder(push, pop1);
boolean b2 = stackPopOrder.isPopOrder(push, pop2);
System.out.println(b1);
System.out.println(b2);
}假如入栈顺序是[1, 2, 3, 4, 5]举个出栈顺序正确的例子[4, 5, 3, 2, 1]:
| 操作 | 辅助栈 | 出栈 |
|---|---|---|
| 压入1 | 1 | |
| 压入2 | 1, 2 | |
| 压入3 | 1, 2, 3 | |
| 压入4 | 1, 2 ,3 ,4 | |
| 弹出4 | 1,2 ,3 | 4 |
| 压入5 | 1,2, 3 ,5 | |
| 弹出5 | 1, 2, 3 | 5 |
| 弹出3 | 1,2 | 3 |
| 弹出2 | 1 | 2 |
| 弹出1 | 1 |
再举个错误的出栈顺序的例子[4,3,5,1,2]
| 操作 | 辅助栈 | 出栈 |
|---|---|---|
| 压入1 | 1 | |
| 压入2 | 1, 2 | |
| 压入3 | 1, 2, 3 | |
| 压入4 | 1, 2 ,3 ,4 | |
| 弹出4 | 1,2 ,3 | 4 |
| 弹出3 | 1, 2 | 3 |
| 压入5 | 1, 2, 5 | |
| 弹出5 | 1, 2 | 5 |
| 弹出2 | 2 | |
| 弹出1 | 1 |
最后只剩两个元素1, 2时,由于2在栈顶1在栈底,不能先弹出1在弹出2,所以这个出栈顺序是错误的。
- 功能测试(输入的两个数组含有多个数字或者只有一个数字;第二个数组是或者不是第一个数组表示的压入序列对应的栈和弹出序列)。
- 特殊输入测试(输入两个null)
题目一:不分行从上到下打印二叉树
从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。
private ArrayList<Integer> printFromTopToBottom(TreeNode root) {
ArrayList<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
TreeNode node = null;
while (!queue.isEmpty()) {
node = queue.poll();
result.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
return result;
}先将根结点入列,出列并打印然后按照从左到右的顺序依次将该结点的子结点入列....不断重复这个过程直到队列为空。
- 功能测试(完全二叉树;所有节点只有左子树的二叉树;所有节点只有右子树的二叉树)。
- 特殊输入测试(二叉树根节点为null;只有一个节点的二叉树)。
从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。
和上面类似,现在要求每打印完树的一层需要换行。核心代码其实和上面一样。只是为了确定在何时需要换行操作,需要用两个变量记录当前层还没有被打印的结点数、下层总结点数。每打印完一行后需要换行,接下来要打印下一层了,所以用下层总结点数更新当前层未被打印的结点数,同时下层总结点数重置为0,准备进行下一层的计数。
private void printTreeEveryLayer(TreeNode root) {
if (root == null) {
return;
}
//下一层节点数
int nextLevel = 0;
//本层未打印节点数,第一层还未打印。故初始化为1
int toBePrint = 1;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
TreeNode node = null;
while (!queue.isEmpty()) {
node = queue.poll();
System.out.print(node.val + " ");
toBePrint--;
if (node.left != null) {
queue.offer(node.left);
nextLevel++;
}
if (node.right != null) {
queue.offer(node.right);
nextLevel++;
}
if (toBePrint == 0) {
System.out.println();
toBePrint = nextLevel;
nextLevel = 0;
}
}
}请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打针,第三行再按照从左到右的顺序打印,其他行以此类推,
举个例子,下面的二叉树,打印顺序是1 3 2 4 5 6 7
1
/ \
2 3
/ \ / \
4 5 6 7
先搞清楚要求:根结点先被打印,然后从右往左打印第二行,接着从左往右打印第三行...以此类推,总之偶数层就从右往左打印,奇数行就从左到右打印。依然需要某种数据结构来存放结点,栈可以满足我们的打印顺序:当前层为奇数层时,按照从左到右的顺序将下层结点(偶数层)压入栈中,出栈的时候就是从右往左打印偶数层了;当前层是偶数层时,按照从右到左的顺序将下层结点(奇数层)压入栈中,由于此时先出栈的是偶数层最右边的结点,所以可以保证下层最右边的结点被压到了栈底,而最左边的结点位于栈顶,出栈的时候就是从左往右打印奇数层了...如此反复交替。
为了达到上述的交替效果,需要用到两个栈,一个栈stackOdd存奇数层的结点,另一个栈stackEven存偶数层的结点。
- 奇数层,其下层的结点按左到右的顺序入栈
- 偶数层,其下层的结点按右到左的顺序入栈
奇偶层顺序是固定的,即根结点是奇数层,则奇偶顺序是“奇偶奇偶....“
stackOdd存放的是某一奇数层的全部结点,stackOdd不为空说明当前层是奇数层,全部弹出后为空,该处理下一层了;因此当stackOdd为空时当前层必然是偶数层,stackOdd就这样不断为空,不为空...交替,正好反映了当前层是奇数层还是偶数层,进而采取不同的结点存入顺序即可。
public static void printTreeZ(TreeNode root) {
if (root == null) {
return;
}
LinkedList<TreeNode> stackOdd = new LinkedList<>();
LinkedList<TreeNode> stackEven = new LinkedList<>();
TreeNode node = null;
stackOdd.push(root);
while (!stackOdd.isEmpty() || !stackEven.isEmpty()) {
if (!stackOdd.isEmpty()) {
while (!stackOdd.isEmpty()) {
node = stackOdd.pop();
System.out.print(node.val + " ");
if (node.left != null) {
stackEven.push(node.left);
}
if (node.right != null) {
stackEven.push(node.right);
}
}
}else {
while (!stackEven.isEmpty()) {
node = stackEven.pop();
System.out.print(node.val + " ");
if (node.right != null) {
stackOdd.push(node.right);
}
if (node.left != null) {
stackOdd.push(node.left);
}
}
}
System.out.println();
}
}题目:输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回true,否则返回false,假设输入的数组的任意两个数字都互不相同。例如。输入数组(5,7,6,9,11,10,8},则返回true,因为这个整数良列是图4.9二叉搜索树的后序遍历结果。如果输入的数组是{7,4,6,5},由于没有哪棵二叉搜索树的后序遍历结果是这个序列,因此返回false。
8
6 10
5 7 9 11
注意是二叉搜索(查找)树,特点是父结点的左子树都比父结点小,父结点的右子树都比父结点大。因此其后序遍历的序列有一定的规律:
- 序列最后一位必然是树的根结点;
- 序列前部分是根结点的左子树,后部分是根结点的右子树;具体来说:将序列各个元素和和序列最后一位的根结点比较,序列前部分都小于根结点的值,这部分子序列是左子树;序列后部分的值都大于根结点,这部分子序列是右子树;
public class VerifySquenceOfBST {
public boolean verify(int[] post) {
if (post == null || post.length <= 0) {
return false;
}
return isSearchBST(post, 0, post.length - 1);
}
private boolean isSearchBST(int[] post, int begin, int end) {
if (begin >= end) {
return true;
}
int root = post[end];
//在二叉搜索树中左子树节点的值小于根节点的值
int i = 0;
for (; i < end; i++) {
if (post[i] > root) {
break;
}
}
//在二叉搜索树中右子树节点的值大于根节点的值
int j = i;
for (; j < end; j++) {
if (post[j] < root) {
return false;
}
}
//判断左子树是不是二叉搜索树
boolean left = true;
if (i > 0) {
left = isSearchBST(post, begin,i-1);
}
//判断左子树是不是二叉搜索树
boolean right = true;
if (j < end - 1) {
right = isSearchBST(post, i, j);
}
return left && right;
}
public static void main(String[] args) {
int[] post1 = {5, 7, 6, 9, 11, 10, 8};
int[] post2 = {7, 4, 6, 5};
int[] post3 = {7};
VerifySquenceOfBST vb = new VerifySquenceOfBST();
System.out.println(vb.verify(post1));
System.out.println(vb.verify(post2));
System.out.println(vb.verify(post3));
}
}题目:输入一棵二叉树和一个整数,打印出二叉树中节点值的和为输入整数的所有路径,从树的根节点开始往下一直到叶节点所经过的节点形成一条路径,
二叉树节点的定义如下:
public class TreeNode {
public int val = 0;
public TreeNode left = null;
public TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}当用前序遍历的方式访问到某一节点时,我们把该节点添加到路径上,并累加该节点的值。如果该节点为叶节点,并且路径中节点值的和刚好等于输入的整数,则当前路径符合要求,我们把粌打印出来。如果当前节点不是叶节点,则继续访问它的子节点。当前节点访问结束后,递归函数将自动回到它的父节点。因此,我们在函数退出之前要在路径上删除当前节点并减去当前节点的值,以确保返回父节点时路径刚好是从根节点到父节点。我们不难看出保存路径的数据结构实际上是一个栈,因为路径要屯递归调用状态一致,而递归调用的本质就是一个压栈和出栈的过程。
public class FindPath {
public ArrayList<ArrayList<Integer>> findPath(TreeNode root, int target) {
ArrayList<ArrayList<Integer>> result = new ArrayList<>();
if (root == null) {
return result;
}
ArrayList<Integer> path = new ArrayList<>();
preOrder(root, target, path, result);
return result;
}
private void preOrder(TreeNode root, int curValue, ArrayList<Integer> path, ArrayList<ArrayList<Integer>> result) {
if (root == null) {
return;
}
//模拟节点进栈
path.add(root.val);
curValue -= root.val;
// 只有在叶子结点处才判断是否和目标值相同,若相同加入列表中
if (root.left == null && root.right == null) {
if (curValue == 0) {
result.add(new ArrayList<>(path));
}
}
preOrder(root.left, curValue, path, result);
preOrder(root.right, curValue, path, result);
path.remove(path.size() - 1);
curValue += root.val;
}
public static void main(String[] args) {
FindPath fp = new FindPath();
TreeNode root = new TreeNode(10);
TreeNode root1 = new TreeNode(5);
TreeNode root2 = new TreeNode(12);
TreeNode root3 = new TreeNode(4);
TreeNode root4 = new TreeNode(7);
root.left = root1;
root.right = root2;
root1.left = root3;
root1.right = root4;
ArrayList<ArrayList<Integer>> res = fp.findPath(root, 22);
System.out.println(res);
}
}- 功能测试(二叉树中有一条,或多条符合要求的路径;二叉树中没有符合要求的路径)。
- 特殊输入测试(指向二叉树根节点的指针为null)。
题目:请实现函数ComplexListNode Clone(ComplexListNode head),复制一个复杂链表,在复杂链表中,每个节点除了有一个next指针指向下一全邛是,还有一个sibling指针指向链表中的任意节点或者null
节点定义如下:
public class RandomListNode {
int label;
RandomListNode next = null;
RandomListNode random = null;
RandomListNode(int label) {
this.label = label;
}
}**注意不可将链表头结点引用返回,所以需要自己new一个结点出来。**要完成复杂链表的复制,第一步要完成普通链表的复制,普通链表的复制可以用一个栈复制每一个结点,之后逐个弹出并连接起来。对于本题有两种策略:
第一种是,在复制普通链表时,将原链表结点和复制链表的结点成对存入HashMap<N, N'>中,建立一对一的映射。当进行随机结点复制时,遍历原链表,如果某结点的随机结点不为空,那么根据HashMap能以O(1)的时间找到对应的复制链表结点中,若原始链表的结点M指向随机结点S,那么复制链表的M'也要指向结点S',这种方法时间复杂度为O(N),但空间复杂度为O(N)。
更好的方法是,插入、连接、拆分三步法。
- 插入:在原始链表的每个结点后插入一个值和它一样的新结点;则有
oriNode.next == cloneNode这样的关系; - 连接随机结点:遍历插入新结点后的链表,在访问原始链表中的那些结点时,判断其是否有随机结点,有的话
cloneNode.random = oriNode.random.next这里oriNode.random.next表示原始链表随机结点的下一个结点,其实就是复制链表的随机结点。 - 拆分原始链表和复制链表:将奇数结点相连就是原始链表,将偶数结点相连就是我们想要的复制链表。返回复制链表的头结点即可。
public class CloneNodes {
public RandomListNode cloneNodes(RandomListNode head) {
if (head == null) {
return null;
}
RandomListNode pNode = head;
//复制结点
while (pNode != null) {
RandomListNode pClone = new RandomListNode(pNode.label+"'");
pClone.next = pNode.next;
pNode.next = pClone;
pNode = pClone.next;
}
//设置每个复制结点的random
pNode = head;
while (pNode != null) {
if (pNode.random != null) {
pNode.next.random = pNode.random.next;
}
pNode = pNode.next.next;
}
//拆分链表
pNode = head;
RandomListNode cloneHead = pNode.next;
RandomListNode pcloneNode = cloneHead;
while (pNode != null) {
pNode.next = pNode.next.next;
if (pcloneNode.next != null) {
pcloneNode.next = pcloneNode.next.next;
}
pNode = pNode.next;
pcloneNode = pcloneNode.next;
}
return cloneHead;
}
public static void main(String[] args) {
CloneNodes cn = new CloneNodes();
RandomListNode r1 = new RandomListNode("A");
RandomListNode r2 = new RandomListNode("B");
RandomListNode r3 = new RandomListNode("C");
RandomListNode r4 = new RandomListNode("D");
RandomListNode r5 = new RandomListNode("E");
r1.next = r2;
r2.next = r3;
r3.next = r4;
r4.next = r5;
RandomListNode head = cn.cloneNodes(r1);
while (head != null) {
System.out.println(head.label);
head = head.next;
}
}
}- 功能测试(节点中的sibling指向节点自身:两个节点的sibling形成环状结构;链表中只有一个节点)
- 特殊输入测试(指向链表头节点的指针为null指针)
题目:输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。 比如,输入图中左边的二叉搜索树,则输出转换之后的排序双向链表。
10
6 14 ===> 4 <==> 6 <==> 8 <==> 10 <==>12 <==> 14 <==> 16
4 8 12 16
二叉树节点定义如下:
public class TreeNode {
public int val = 0;
public TreeNode left = null;
public TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}看到这道题我第一反映就是,二叉树的线索化,不过还是有些区别的,下面会讨论。按照二叉搜索树的特点,最左边的结点是值最小的,而题目要求得到排序的双向链表,所以基本确定下来中序遍历的方法。
二叉树的线索化:是针对每个叶子结点,为了将空指针利用起来,可以将叶子结点的左子结点指向其遍历顺序的前驱,右子结点指向遍历序列的后继。根据遍历顺序的不同,线索化也分为前序、中序、后序。二叉树的结点定义中需要加入布尔变量,用来标示每个结点的左右指针是否被线索化了(这些标志只可能在叶子结点为true)
public class Convert {
private TreeNode preNode;
public TreeNode convert(TreeNode root) {
if (root == null) {
return null;
}
TreeNode pRoot = root;
//得到双向链表
convertNode(root);
//向左找到双向链表的头结点
while (root.left != null) {
root = root.left;
}
return root;
}
//中序遍历改变指针
private void convertNode(TreeNode root) {
if (root == null) {
return;
}
convertNode(root.left);
root.left = preNode;
if (preNode != null) {
preNode.right = root;
}
preNode = root;
convert(root.right);
}
public static void main(String[] args) {
Convert convert = new Convert();
TreeNode r1 = new TreeNode(10);
TreeNode r2 = new TreeNode(6);
TreeNode r3 = new TreeNode(14);
TreeNode r4 = new TreeNode(4);
TreeNode r5 = new TreeNode(8);
TreeNode r6 = new TreeNode(12);
TreeNode r7 = new TreeNode(16);
r1.left = r2;
r1.right = r3;
r2.left = r4;
r2.right = r5;
r3.left = r6;
r3.right = r7;
TreeNode res = convert.convert(r1);
while (res != null) {
System.out.println(res.val);
res = res.right;
}
}
}最后因为需要返回双向链表的头结点,只需从二叉树的根结点开始,向左遍历,即可找到双向链表的头结点。
- 功能测试(输入的二叉树是完全二叉树;所有节点都没有左/右子树的二叉树;只有一个节点的二叉树)。
- 特殊输入测试(批向二叉树根节点的指针为null)
题目:请实现五肉个函数,分别用来序列化和反序列化二叉树。
刚开始想法太死板了,只记得中序和前序或者中序和后续两个序列才能决定一棵唯一的二叉树,于是分别进行了前序、中序遍历,前序和中序的序列用"|"分隔,之后再根据这个分隔符分成前序和中序序列,最后采用面试题7——重建二叉树的思路进行反序列化。思路是正确的但是太麻烦。
其实遇到空指针可以也用一个特殊的字符表示,比如“#”,这样前序遍历序列就可以表示唯一的一棵二叉树了。对于空指针也用一个字符表示,可称这样的序列为扩展序列。而二叉树的建立,必须先要建立根结点再建立左右子树(root为空怎么调用root.left是吧),所以必须前序建立二叉树,那么序列化时也应该用前序遍历,保证了根结点在序列前面。
不能使用中序遍历,因为中序扩展序列是一个无效的序列,比如
A B
/ \ \
B C 和 A 中序扩展序列都是 #B#A#C#
\
C
先来看序列化的代码,其实就是在前序遍历的基础上,如果遇到空指针就用“#”表示。
public String serialize(TreeNode root) {
if (root == null) {
return null;
}
StringBuilder sb = new StringBuilder();
preOrxder(root, sb);
return sb.toString();
}
private void preOrxder(TreeNode root, StringBuilder sb) {
if (root == null) {
sb.append("# ");
return;
}
sb.append(root.val).append(" ");
preOrxder(root.left, sb);
preOrxder(root.right, sb);
}再来看反序列化,通过前序遍历得到的字符串,重建二叉树。
private TreeNode deSerialize(String sb) {
if (sb == null || sb.length() == 0) {
return null;
}
String[] seq = sb.split("\\s");
return reconstructBST(seq);
}
private int index = -1;
private TreeNode reconstructBST(String[] seq) {
index++;
if (seq.length == 0) {
return null;
}
//注意这里的写法
if (seq[index].equals("#")) {
return null;
}
TreeNode root = new TreeNode(Integer.parseInt(seq[index]));
root.left = reconstructBST(seq);
root.right = reconstructBST(seq);
return root;
}由于前序遍历时每存入一个结点值或者存入“#”后面都紧跟着一个空格。所以最后得到的序列时这样的格式A B # # C # #,可以根据空格将其分割成[A, B, #, #, C, #, #]这样就还原了各个结点的值,根据这些值重建二叉树。由于得到的是二叉树的前序序列,因此也要以前序重建二叉树,当遇到结点值是“#”时说明这是一个空指针,那么返回null给上层的父结点。如果不为“#”就递归地重建该结点的左右子树。注意这里使用了一个int型的index,用于表示当前结点在String[] seq中的索引,无需担心index在seq中会造成数组下标越界,因为最后一个结点的左右子树肯定是null,必然会终止递归。
public static void main(String[] args) {
TreeNode r1 = new TreeNode(1);
TreeNode r2 = new TreeNode(2);
TreeNode r3 = new TreeNode(3);
TreeNode r4 = new TreeNode(4);
TreeNode r5 = new TreeNode(5);
TreeNode r6 = new TreeNode(6);
r1.left = r2;
r1.right = r3;
r2.left = r4;
r3.left = r5;
r3.right = r6;
SerializeBT sb = new SerializeBT();
String str = sb.serialize(r1);
System.out.println(str);
TreeNode r = sb.deSerialize(str);
System.out.println(r);
}- 功能测试(输入的二叉树是完全二叉树;所有节点都没能左/右子树的二叉树;只有一个节点的二叉树;所有节点的值都相同的二叉树)。
- 特殊输入测试(批向二叉树根节点的指针为null)
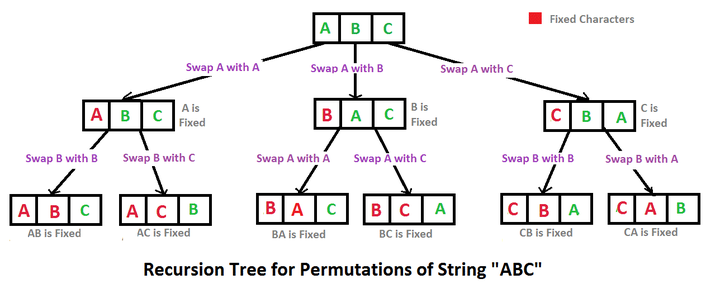
题目:输入一个字符串,打印出该字符串中字符的所有排列。
例如:输入字符串abc,则打印出由字符a、b、c所能排列出来的甩有字符串abc、acb、bac、bca、cab和cba
public class Permutation {
public static ArrayList<String> permutation(String str) {
ArrayList<String> result = new ArrayList<>();
if (str == null || str.length() == 0) {
return result;
}
permutationCore(str.toCharArray(), 0, result);
Collections.sort(result);
return result;
}
private static void permutationCore(char[] chars,int begin, ArrayList<String> result) {
if (begin == chars.length - 1) {
String s = String.valueOf(chars);
if (!result.contains(s)) {
result.add(s);
return;
}
}
for (int i = begin; i < chars.length; i++) {
swap(chars, begin, i);
permutationCore(chars, begin + 1, result);
//交换后再交换回来
swap(chars, i, begin);
}
}
private static void swap(char[] chars, int i, int j) {
char temp = chars[i];
chars[i] = chars[j];
chars[j] = temp;
}
public static void main(String[] args) {
ArrayList<String> result = permutation("abc");
for (String s : result
) {
System.out.println(s);
}
}
}- 功能测试(输入的字符串中有一个或者多个字符)。
- 特殊输入测试(输入的字符串的内容为空或者null)
如果要求字符的所有组合呢?比如abc,所有组合情况是[a, b, c, ab, ac, bc, abc],包含选择1个、2个、3个字符进行组合的情况,即
$$
\sum{C_3^1 + C_3^2 + C_3^ 3}
$$
。这可以用一个for循环完成。所以关键是如何求得在n个字符里选取m个字符总共的情况数,即如何求C(n, m)
n个字符里选m个字符,有两种情况:
- 第一个字符在组合中,则需要从剩下的n-1个字符中再选m-1个字符;
- 第一个字符不在组合中,则需要从剩下的n-1个字符中选择m个字符。
上面表达的意思用数学公式表示就是 $$ C_n^m = C_{n-1}^{m-1} + C_{n-1}^m $$
全排列的过程:
- 选择第一个字符
- 获得第一个字符固定下来之后的所有的全排列
- 选择第二个字符
- 获得第一+ 二个字符固定下来之后的所有的全排列
从这个过程可见,这是一个递归的过程。
public class Permutation2 {
public static ArrayList<String> permutation2(String str) {
ArrayList<String> result = new ArrayList<>();
if (str == null || str.length() == 0) {
return result;
}
StringBuilder sb = new StringBuilder();
for (int i = 1; i <= str.length(); i++) {
permutationCore(str, i,sb, result);
}
return result;
}
private static void permutationCore(String str, int num, StringBuilder sb ,ArrayList<String> list) {
if (num == 0) {
if (!list.contains(sb.toString())) {
list.add(sb.toString());
return;
}
}
if (str.length() == 0) {
return;
}
// 公式C(n, m) = C(n-1, m-1)+ C(n-1, m)
// 第一个字符是组合中的第一个字符,在剩下的n-1个字符中选m-1个字符
sb.append(str.charAt(0)); //选中第一个字符
permutationCore(str.substring(1), num - 1, sb, list);
// 第一个字符不是组合中的第一个字符,在剩下的n-1个字符中选m个字符
sb.deleteCharAt(sb.length() - 1);
permutationCore(str.substring(1), num, sb, list);
}
public static void main(String[] args) {
ArrayList list1 = permutation2("abc");
System.out.println(list1);
ArrayList list2 = permutation2("abcca");
System.out.println(list2);
}
}题目:输入一个含有8个数字的数组,判断有没有可能把这8个数字分别放到正方体的8个顶点上,使得正方体上三组相对的面上的4个顶点的和都相等。
这相当于先得到a1、a2、a3、a4、a5、a6、a7和a8这8数字的所有排列,然后判断有没有某一个排列符合题目给定的条件,即a1+a2+a3+a4 = a5+a6+a7+a8,a1+a3+a5+a7 = a2+a4+a6+a8.并且 a1+ a2+a5+a6=a3+a4+a7+a8
public class Permutation3 {
public static ArrayList<int[]> possibilitiesOfCube(int[] array) {
ArrayList<int[]> list = new ArrayList<>();
if (array == null || array.length != 8) {
return list;
}
ArrayList<int[]> result = new ArrayList<>();
permutation(array, 0, list);
if (list.size() > 0) {
for (int[] a : list) {
if (check(a)) {
result.add(a);
}
}
}
return result;
}
private static void permutation(int[] array, int begin, ArrayList<int[]> result) {
if (begin == array.length - 1) {
if (!has(result, array)) {
result.add(Arrays.copyOf(array, array.length));
return;
}
}
for (int i = begin; i < array.length; i++) {
swap(array, i, begin);
permutation(array, begin + 1, result);
swap(array, i, begin);
}
}
private static void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
/**
* list中的数组是包含array
*
* @param list
* @param array
* @return
*/
private static boolean has(ArrayList<int[]> list, int[] array) {
for (int i = 0; i < list.size(); i++) {
if (equal(list.get(i), array)) {
return true;
}
}
return false;
}
/**
* array1是否与array2值相等
*
* @param array1
* @param array2
* @return
*/
private static boolean equal(int[] array1, int[] array2) {
for (int i = 0; i < array1.length; i++) {
if (array1[i] != array2[i]) {
return false;
}
}
return true;
}
/**
* 判断各边和是满足要求
*
* @param array
* @return
*/
private static boolean check(int[] array) {
if (array[0] + array[1] + array[2] + array[3] == array[4] + array[5] + array[6] + array[7]
&& array[0] + array[2] + array[4] + array[6] == array[1] + array[3] + array[5] + array[7]
&& array[0] + array[1] + array[4] + array[5] == array[2] + array[3] + array[6] + array[7]) {
return true;
}
return false;
}
public static void main(String[] args) {
int[] a = {1, 1, 2, 2, 3, 3, 4, 4};
int[] A = {1,2,3,1,2,3,2,2};
int[] B = {1,2,3,1,8,3,2,2};
List<int[]> list = possibilitiesOfCube(B);
System.out.println("有" + list.size() + "种可能");
for (int[] arr : list) {
System.out.println(Arrays.toString(arr));
}
}
}题目:数组中有一个数字出现的次数超过数组长度的一半,请找出为个数字。
例如,输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了4次,超过数组长度的一半,因此输出2。
可以先将数组排序,然后统计数字出现的次数,先将第一个数字出现次数初始化为1,如果遇到同样的数字,就加1,遇到不一样的就重新初始化为1重新开始计数,直到某个数字计数值大于n / 2(n是数组的长度),终止循环,返回当前数字就是我们要的答案。
但是排序算法的时间复杂度为O(nlgn),有没有更快的方法呢。
**注意到排序之后,如果数组中存在某个数字超过数组长度的一半,那么数组中间的数字必然就是那个出现次数超过一半的数字。**这就将问题转化成了求数组的中位数,快速排序使用的切分算法可以方便地找出中位数,且时间复杂度为O(n),找出中位数后还需要再遍历一边数组,检查该中位数是否出现次数超过数组长度的一半。总结一下,基于切分法有如下两个步骤:
- 切分法找出中位数
- 检查中位数
/**
* 使用快速排序思想,切分法。时间复杂度o(n)
* @param nums
* @return
*/
public int moreThanHalfNum2(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int k = nums.length / 2;
int low = 0;
int high = nums.length - 1;
while (high > low) {
int j = partition(nums, low, high);
if (j == k) {
return nums[k];
} else if (j < k) {
low = j + 1;
} else {
high = j - 1;
}
}
//检查
return check(nums, nums[k]) ? nums[k] : 0;
}
/**
* 快速排序切分
* @param nums
* @param low
* @param high
* @return
*/
private int partition(int[] nums, int low, int high) {
int i = low;
int j = high;
if (i < j) {
int piv = nums[low];
while (i < j) {
while (nums[j] > piv) {
j--;
}
if (i < j) {
nums[i] = nums[j];
i++;
}
while (nums[i] < piv) {
i++;
}
if (i < j) {
nums[j] = nums[i];
j--;
}
}
nums[i] = piv;
}
return i;
}数组中有一个数字出现次数超过了一半,说明这个数字的出现次数比其他所有数字的出现次数之和加起来还要多。于是可以考虑下面的方法:使用两个变量,result表示当前数字,count表示当前数字的计数值。在遍历到一个新的数字时候,计数为1,将该数字赋值给result,之后遇到的数字如果和result相同,那么count加1,;遇到不一样的count减1,直到count等于0,此时需要重新初始化,即将新的数字赋值给result并令count为1......这样遍历完所有数字时,最后result表示的数值就可能是我们要找的值,注意是可能,因为输入数组可能本身就不满足里面有某个数字出现次数超过一半。因此和上面的找中位数方法一样,得到的result还需要进一步检验。
public class MoreThanHalfNum {
public int moreThanHalfNum1(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
//计数器
int count = 0;
//表示当前数字
int result = nums[0];
for (int i = 0; i < nums.length; i++) {
if (result == nums[i]) {
count++;
}else {
count--;
if (count == 0) {
count++;
result = nums[i];
}
}
}
return check(nums, result) ? result : 0;
}
private boolean check(int[] nums, int result) {
int count = 0;
for (int num : nums) {
if (num == result) {
count++;
}
}
return count > nums.length / 2;
}
}
public static void main(String[] args) {
MoreThanHalfNum mthn = new MoreThanHalfNum();
int[] nums1 = {1, 2, 3, 2, 2, 2, 5, 4, 2};
int[] nums2 = {1,2};
System.out.println(mthn.moreThanHalfNum2(nums1));
System.out.println(mthn.moreThanHalfNum2(nums2));
System.out.println("**********");
System.out.println(mthn.moreThanHalfNum1(nums1));
System.out.println(mthn.moreThanHalfNum1(nums2));
}
}- 功能测试(输入的数组中存在一个出现次数超过数组长度一半的数字;输入的数组中不契在一个出现次数超过数组长度一半的数字)。
- 特殊输入测试(输入的数组中只有一个数字‘;输入null)。
题目:输入n个整数,找出其中最小的k个数。
例如,输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4
如果做了面试题39,这道题很容易想到直接使用切分法。几乎一模一样的代码。注意k的取值范围,不能比输入数组的长度还要大,也不能为非正数。
采用这种思路是有限制的,我们需要修改输入的数组,因为函数Partition会调整数组中数字的顺序,如果面试官要求不能修改输入的数组,那我们该怎么办呢?
有一个很简单的想法:设想有一个容器,其大小不超过k时,就不断存入元素,只要容量超过k,就剔除其中最大的元素,重复该过程,当遍历所有元素后,该容器中剩下的刚好就是最小的k个元素。
哪种容器能快速得到最大元素,可能第一想到的就是最大堆。
上面的方法还是太麻烦了,面试了哪有那么多时间让你手写一个堆和一大堆代码的切分方法。而且上述两种方法都改变了原数组。Java内置了优先队列,就是基于堆实现的,默认是最小堆,可以传入Comparator改变堆的形式。
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b.compareTo(a)); // 注意参数a、b的顺序和compareTo方法中a、b的位置
// 或者直观的写法
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reversOrder());public class GetLeastNumbers {
public ArrayList<Integer> getLeastNumbers(int[] arrays, int k) {
ArrayList<Integer> list = new ArrayList<>();
if (arrays == null || arrays.length == 0 || k <= 0 || k > arrays.length) {
return list;
}
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
for (int a : arrays) {
maxHeap.offer(a);
//只要size大于k,不断剔除最大值,最后优先队列里只剩最小的k个
if (maxHeap.size() > k) {
maxHeap.poll();
}
}
list.addAll(maxHeap);
return list;
}
public static void main(String[] args) {
GetLeastNumbers gln = new GetLeastNumbers();
int[] arrays = {4, 5, 1, 6, 2, 7, 3, 8};
ArrayList list = gln.getLeastNumbers(arrays, 4);
System.out.println(list);
}
}优先队列可以以O(1)的时间删除堆顶元素,但是由于删除后还要恢复堆有序状态,而优先队列的大小不会超过k + 1,因此时间复杂度为O(lg k)。又由于输入中有n个数,故总的时间复杂度为O(nlgk)。
优先队列中的元素从来不会超过k + 1,因此即使有海量的数据不用担心,因为无需将海量数据一次性加载进内存,只需要每次读取一个值,然后剔除一个最大值,优先队列的大小将长期稳定在k。
比较一下这几个方法,切分法是最快的,但是不适合用于处理海量数据;基于优先队列的实现虽然速度满了点但是可以进行海量数据处理,看具体应用场景了。
- 功能测试(输入的数组中有相同的数字;输入的数组中没有相同的数字)
- 边界值测试(输入的k等于1或者等于数组的长度)
- 特殊输入测试(k小于1;k大于数组的长度;指向数组的指针为null)
题目:如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后是间两个数的平均值。
这道题的意思是,有一个容器不断接收到流中的数据,因此该容器的大小是动态的,找出一种方法能快速得到动态容器中的中位数。
最容易想到的就是直接对容器排序,中位数就是中间的元素。但是时间复杂度为O(nlgn)太高了;
使用切分算法对一个数组进行部分排序,能以O(n)的时间找出中位数,插入容器中的时间是O(1);
使用有序数组,因为插入时候要将插入位置后的所有元素后移一位,所以时间复杂度为O(n),但是对于始终保持有序的数组来说,要找出中位数只需O(1)的时间;
使用二叉查找树可以实现以平均O(lgn)时间插入和获取,最差情况下:二叉树极度不平衡,树退化成链表,此时时间复杂度变高到了O(n)。
有没有更好的办法呢?
中位数将数组分成两部分,**中位数左边的部分比中位数右边的部分都要小,换言之:左边部分的最大值也不会超过右边部分的最小值。**要获取最大值、最小值,比较容易想到的就是最大堆和最小堆了。又注意到,被中位数分开的两个部分,其大小之差不会超过1。所以在往两个堆里存入元素时,要保证交替存入两个容器,比如:当前元素个数为奇数时,就默认存入最小堆中;当前元素个数为偶数时,就默认存入最大堆中;当前没有元素时,默认存入最大堆中。
为了保证中位数左边部分的最大值也不会超过右边部分的最小值,**应该使用最大堆存放较小元素,最小堆存放较大元素。**有两种特殊情况:
- 当前要存入最大堆中的元素比最小堆的最小值大,这样不能保证最大堆的最大值不会超过最小堆的最小值。此时需要将最小堆中的最小值弹出并存入最大堆中,并将当前元素存入最小堆中,其实就是将当前元素和最小堆的最小值交换了存储位置。
- 当前要存入最小堆的元素比最大堆的最大值小,这样也不能保证最大堆的最大值不会超过最小堆的最小值。此时需要将最大堆中的最大值弹出并存入最小堆中,并将当前元素存入最大堆中。
中位数的获取就很简单了,如果当前数据流中个数为奇数,则中位数一定是最大堆的最大值(因为上面规定了当前数据个数为偶数时存入最大堆中,之后数据个数变成奇数,因此要么最大堆的大小比最小堆一样,要么比最小堆大1);如果当前数据流中个数为偶数,那么要求平均数,这两个中间值一个是最大堆的最大值,一个是最小堆的最小值。
下面来比较下各个方法的效率。
| 数据结构 | 插入复杂度 | 得到中位数的复杂度 |
|---|---|---|
| 没有排序的数组 | O(1) | O(n) |
| 有序数组 | O(n) | O(1) |
| 排序的链表 | O(n) | O(1) |
| 二叉查找树 | 平均O(lgn),最差O(n) | 平均O(lgn),最差O(n) |
| 最大堆、最小堆 | O(lg n) | O(1) |
public class MedianInStream {
private PriorityQueue<Integer> maxPQ = new PriorityQueue<>(Comparator.reverseOrder());
private PriorityQueue<Integer> minPQ = new PriorityQueue<>();
private int count;
public void insert(Integer num) {
//第一个元素插入最大堆
if (count == 0) {
maxPQ.offer(num);
}//当前数据流为奇数个时,存入最小堆
else if ((count & 1) == 1) {
//如果存入最小堆的元素比最大堆的最大元素要小,,将不能保证最小堆的最小元素大于最大堆的最大元素
//此时需要将最大堆的最大元素给最小堆,然后将这个元素存入最大堆中
if (num < maxPQ.peek()) {
minPQ.offer(maxPQ.poll());
maxPQ.offer(num);
} else {
minPQ.offer(num);
}
}//当前数据流为偶数个时,存入最大堆
else if ((count & 1) == 0) {
// 如果要存入最大堆的元素比最小堆的最小元素大,将不能保证最小堆的最小元素大于最大堆的最大元素
// 此时需要将最小堆的最小元素给最大堆,然后将这个元素存入最小堆中
if (num > minPQ.peek()) {
maxPQ.offer(minPQ.poll());
minPQ.offer(num);
} else {
maxPQ.offer(num);
}
}
count++;
}
public Double getMedian() {
// 当数据流读个数为奇数时,最大堆的元素个数比最小堆多1,因此中位数在最大堆中
if ((count & 1) == 1) {
return Double.valueOf(maxPQ.peek());
}
// 当数据流个数为偶数时,最大堆和最小堆的元素个数一样,两个堆的元素都要用到
System.out.println(maxPQ.peek());
System.out.println(minPQ.peek());
return (Double.valueOf(maxPQ.peek()) + Double.valueOf(minPQ.peek())) / 2;
}
public static void main(String[] args) {
MedianInStream medianInStream = new MedianInStream();
medianInStream.insert(1);
medianInStream.insert(2);
medianInStream.insert(3);
medianInStream.insert(4);
medianInStream.insert(5);
medianInStream.insert(6);
System.out.println(medianInStream.getMedian());
}
}题目:输入一个整型数组,数组里有正数也有负数,数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值,要求时间复杂度为O(n)
例如,输入的数组为{1,-2,3,10,-4,7,2,-5},和最大的子数组为{3,10,-4,7,2},因此输出为该子数组的和18
首先记录下第一个元素,先假设它为最大和。当1加上-2时变成了-1,再加上3等于2,3前面加了一堆还不如不加,所以应该直接从3开始加,即如果当前累加和是负数,那么它加上当前元素将使得新的累加和比当前元素还要小,此时应该将之前的累加和丢弃,从当前元素开始累加。
按照上述方法,新的累加和为3大于当前最大和,因此最大和更新为3;加10,当前最大和变成13,继续-4,当前累加和为9,并不大于当前最大和,因此最大和不更新;加7、加2,当前和为18,大于最大和,当前最大和更新为18;最后-5,当前累加和为13,不大于最大和18。遍历完毕,返回最大和18.如果搞清楚了上面的思路,可以很容易写出如下代码:
public int findGreatestSumOfSubArray(int[] array) {
if (array == null || array.length == 0) {
return 0;
}
int max = array[0];
int sum = 0;
for (int i = 0; i < array.length; i++) {
sum += array[i];
if (sum > max) {
max = sum;
}
if (sum < 0) {
sum = 0;
}
}
return max;
}- 功能测试(输入的数组中有正数也有负数;输入的数组中全是正数;输入的数组中全是负数)。
- 特殊输入测试(表示数组的指针为null)
题目:输入一个整数n,求1-n这n个整数的十进制表示中1出现的次数。
例如,输入12,1-12这些整数中包含1的数字有1、10、11和12,1一共出现了5次。
public int numberOf1Between1AndN(int n) {
n = Math.abs(n);
StringBuilder sb = new StringBuilder();
for (int i = 1; i <= n; i++) {
sb.append(i );
}
int count = 0;
for (int i = 0; i < sb.length(); i++) {
if (sb.charAt(i) == '1') {
count++;
}
}
return count;
}参考LeetCode
1可以出现在任意一位,比如3245,1出现在个、十、百、千位都可以。只要固定某一位为1,计算出该位是1的所有情况,将固定每一位得到的情况数相加就是最终结果。
要固定某一位为1,可以使用m = 1, 10, 100, 1000....,对n作除、余操作,将输入整数分为高位和低位两部分。举个例子,对于输入n = 3101592,m = 100,如果令a = n / m, b = n % m,将得到a = 31015,b= 92两部分,现在固定百位为1(始终固定a的最低位),即xxxx1xx这样的形式,这样形式的数有多少个呢?
0000 1 00
0000 1 01
.....
0000 1 99
0001 1 00
......
0001 1 99
0002 1 00
......
0002 1 99
......
3101 1 00
......
3101 1 99
为了看得直观,上面刻意将数字从百位处分隔开,对于百位之前的高位数,总共有0000~3101共3102种情况,而每一种情况对应着低位有00~99共100种情况,因此百位为1的情况数是3102*100,也就是(a / 10 + 1) * m种情况。好,现在得到百位为1的情况数了,个位与千位等其他位计算方法和上面类似,只需取不同的m就能将输入的整数分成两部分并固定某一位为1.
接下来m = 1000时,3101592被分成a = 3101和b = 592两部分,现在固定千位为1,但是此时千位本来就是1了,来看和上面有什么不同
000 1 000
......
000 1 999
309 1 000
......
309 1 999
310 1 000
......
310 1 592
可以看到千位前的高位从000~309和上面一样,每一种情况都有000~999种可能,但是到310时,后面最多只能到592,共000~592是593种情况。此时千位为1的情况总数为:310 * 1000 + 593,即当前要被固定的位在输入中本来就是1的话有(a / 10) * m + b + 1种情况。
再看m = 10000,固定万位的情况。a = 310, b = 1592.
00 1 0000
......
00 1 9999
30 1 0000
......
30 1 9999
没有了,共31 * 10000种,即当前要被固定的位在输入中是0的话有(a / 10) * m种情况。
一开始固定百位其实就是当前要被固定的位在输入中是2~9这种情况。
分析得差不多了,现在考虑这三种情况计算就好了。
public int numberOf1Between1AndN2(int n) {
int ones = 0;
for (long m = 1; m <= n; m *= 10) {
long a = n / m;
long b = n % m;
if (a % 10 == 0) {
ones += a / 10 * m;
} else if (a % 10 == 1) {
ones += (a / 10 * m) + (b + 1);
}else {
ones += (a / 10 + 1) * m;
}
}
return ones;
}- 功能测试(输入5,10,55,99等)。
- 边界值测试(输入0,1等)
- 性能测试(输入较大的数字,如10000,21235等)
题目: 数字以0123456789101112131415... 的格式序列化得到一个字符序列中。在这个序列中,第5位(从0开始计数)是5,第13位是1,第19位是4,等等。请写一个函数,求任意第n位对应的数字。
从数字本身的规律入手。如果要找第1001位,肯定不会考虑09这十位吧?接下来10-99也就有180位而已,不考虑,每次不考虑的情况需要减去已缩小查找范围,因此在排除掉0-99共180+10后还剩881,也就是说我们原来是从0开始找到第1001位,现在只需从100开始找到第991位即可。接下来看100-999共2700位,由于881 < 2700,所以这个数必然在100999的范围内。881 = 270 * 3 + 1,说明这个数是100开始之后的第270个数的第1位(从0开始计算索引),也就是370的第一位数,即7。
有了思路后,要实现几个关键的方法,首先是根据位数得到一个区间的开始数字。区间划分为:0-9, 10-99, 100-999...比如n = 1,一位数的开始数是0; n = 2,两位数的开始数是10; n = 3,三位数的开始数是100...
其次因为要缩小查找范围,所以要根据位数知道该范围内总共有多少个数字,比如n = 1, 一位数0-9的范围共10个数;n = 2,两位数10-99的范围共90个数;n = 3,三位数100-999的范围共900个数....
还需要一个方法,一旦锁定范围,根据当前的位数能知道包含index处数字的数是几,然后从该数中找到要求的那位。
public class DigitAtIndex {
public int digitAtIndex(int index) {
if (index < 0) {
return -1;
}
//位数,digits = 1;表示一位数,0-9区间;digjts = 2表示两位数,10-99区间...
int digits = 1;
while (true) {
int numbers = numOfRange(digits);
//范围锁定,numbers*digits表示该区间共有多少位数字,如digits = 2,范围10-99 有 2*90=80位
if (index < numbers * digits) {
return digitAt2(index, digits);
}
//缩小范围
index -= numbers * digits;
digits++;
}
}
/**
* 根据位数得到范围内的个数,比如1位,0-9共10个
* 2位,10-99共90个
* 3们,100-999 共900个
* @param n
* @return
*/
private int numOfRange(int n) {
if (n == 1) {
return 10;
}
return (int)(9 * Math.pow(10, n - 1));
}
/**
* n位数范围内的的第一个数,比如1位数,0~9,第一个是0
* 3位数,100~199,第一个数是100
* @param n
* @return
*/
private int beginNumber(int n) {
if (n == 1) {
return 0;
}
return (int) Math.pow(10, n-1);
}
/**
* 返回某数的第d位,第0位是个位,第1位是十位
* @param value
* @param d
* @return
*/
private int digitAt(int value, int d) {
return (value/(int)Math.pow(10,d))% 10;
}
/**
* 锁定范围后,根据位数就能得到包含index处那位数的数字,然后从该数中找到要求的那位
* @param seqIndex
* @param digits
* @return
*/
private int digitAt2(int seqIndex, int digits) {
int number = beginNumber(digits) + seqIndex / digits;
return digitAt(number, digits - seqIndex % digits - 1);
}
public static void main(String[] args) {
DigitAtIndex a = new DigitAtIndex();
System.out.println(a.digitAtIndex(1001));
}
}题目:输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打针能拼接出的所有数字中最小的一个。
例如,输入数组{3,32,321},慢打印出这3个数字能排成最小数字321323。
这道题可以对数组排序,比如对于普通的数组{23, 12, 32},可能会想到按照自然序排序后,得到{12, 23, 32}然后直接拼接起来就得到了最小的数字122332,但是像题中的例子按照自然序排好后就是{3, 32, 321},如果直接拼接得到332321,是不是最小呢?可以发现排好后是{321, 32, 3},才能得到最小数321323。可见这已经不是自然序了,所以想到需要自定义一种比较方法,得到一种新的排序方式。
既然是要拼接数组中所有的数,保证拼接后的数最小,我们从最小的问题出发,当数组中只有两个数时,情况很简单,比如{3, 32},有用两种方式拼接他们"3"+"32"和"32"+"3",分别为332和323,因为323 < 332,所以将32排在3的前面,也就是对于数组中的任意两个数m和n,如何mn < nm,则应该将m排在n的前面。在Java中很好实现,只需重写一个Comparator即可。使用Java 8的lambda表达式可以简化这一过程。
public class PrintMinNumber {
public String printMinNumber(int[] numbers) {
if (numbers == null || numbers.length == 0) {
return "";
}
List<Integer> list = new ArrayList<>();
for (int a : numbers) {
list.add(a);
}
//a b 比较,小的排在前面
list.sort((a, b) -> (a + "" + b).compareTo(b +a+ ""));
StringBuilder sb = new StringBuilder();
for (int a : list) {
sb.append(a);
}
return sb.toString();
}
public static void main(String[] args) {
PrintMinNumber pm = new PrintMinNumber();
int[] nums = {3, 32, 321};
String res = pm.printMinNumber(nums);
System.out.println(res);
}
}题目:给定一个数字,我们按照如下地铡把它翻译为字符串:0翻译成”a“,1管充成”b“,......,11翻译成”l“。25秒充成”z“。一个数字可能有多个翻译。
例如,12258有5种不同的翻译,分别是”bccfi“,”bwfi“,bczi”,“mcfi”,“mzi”。请编程实现一个函数,用来计算一个数字有多少种不同的翻译方法。
举个简单的例子,比如258,我们可以先翻译第一个数字,得到c,也可以翻译前两个数字,得到z;如果先翻译了一个数,对于剩下的58,和上面一样可以选择只翻译一位,得到f,也可以翻译两位(在这个例子中是不合法的,58没有与之映射的字符),如果先翻译了两位,对于剩下的8,只能有一种翻译方法了,得到i。所以最后得到两种翻译方法,cfi和zi。
从这个简单的例子可以得到一般性的结论,令f(i)为从第i位开始的不同翻译的数目,因为每次可以选择只翻译一个数字,也可一次翻译两个数字,而对于剩下的数字也可以采用同样的方法,这是一个递归问题。 $$ f(i) = f(i+1) + g(i, i+1)f(i+2), 0 \le i < n $$ 其中n为数字的位数, $$ g(i, i+ 1) $$ 可取0或者1,当一次翻译两个数字时,如果这个数字在 $$ 10 \le m \le25 $$ 的范围内,这就是一个可翻译的数,此时 $$ g(i, i + 1) $$ 为1,否则为0。根据题意,我们最后就是要求得 $$ f(0) $$
如果自下而上,从小的结果出发,保存每一步计算的结果,以供下一步使用,也就是我们按照从右到左的顺序翻译。 $$ f(i) = f(i+1) + g(i, i+1)f(i+2), 0 \le i < n $$
对于上面的公式,也就是先求出 $$ f(n -1) $$ ,然后求出 $$ f(n -2) $$ ,之后根据这两个值求出f(n -3),然后根据f(n-2)和f(n -3)求出f(n -4)一直往左知道求出 $$ f(0) $$ ,这就是我们要的结果!
public class TransLateNumToString {
public int transLateNumToString(int n) {
if (n < 0) {
return 0;
}
return count(String.valueOf(n));
}
private int count(String num) {
int len = num.length();
int[] counts = new int[len];
for (int i = len - 1; i >= 0; i--) {
int count = 0;
if (i < len - 1) {
count = counts[i + 1];
} else {
count = 1;
}
if (i < len - 1) {
int digit1 = num.charAt(i)-'0';
int digit2 = num.charAt(i + 1)-'0';
int convertD = digit1 * 10 + digit2;
if (convertD >= 10 && convertD <= 25) {
if (i < len - 2) {
count += counts[i + 2];
} else {
count++;
}
}
}
counts[i] = count;
}
return counts[0];
}
public static void main(String[] args) {
TransLateNumToString ts = new TransLateNumToString();
System.out.println(ts.transLateNumToString(12258));
}
}- 功能测试(只有一位数字:包含多位数字)。
- 特殊输入测试(负数:0;包含25,26的数字)
题目:在一个mxn的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格,直到到达棋盘的右下角。给定一个棋盘及其上面的礼物,请计算你最多能拿到多少价值的礼物?
例如,在下面的棋盘中,如果沿着带下画线的数字的线路(1,12,5,7,7,16,5),那么我们能拿到的最大价值为53的礼物。
1 |
10 | 3 | 8 |
|---|---|---|---|
12 |
2 | 9 | 6 |
5 |
7 |
4 | 11 |
| 3 | 7 |
16 |
5 |
public int getMaxValue(int[][] gifts) {
if (gifts == null || gifts.length == 0) {
return 0;
}
int rows = gifts.length;
int cols = gifts[0].length;
int[] max = {0};
select(gifts, 0, 0, max,rows,cols,0);
return max[0];
}
private void select(int[][] gifts, int row, int col,int[] max,int rows, int cols,int val) {
if (row >= rows || col >= cols) {
return;
}
val += gifts[row][col];
if (row == rows - 1 && col == cols - 1) {
if (val > max[0]) {
max[0] = val;
}
}
select(gifts, row + 1, col, max, rows, cols, val);
select(gifts, row , col+1, max, rows, cols, val);
}每进入一个格子,累加礼物价值。当到达右下角时,将累加和与全局的max变量比较,如果某条路径的累加和比max大,就更新max。边界控制很重要,在超出行或者超出列的范围后,直接返回。然后就不断在两个方向递归——右边或者下边。全局max由于是int型,作为参数并不能在递归调用后被改变,所以需要一个对象,由于只需要存放一个值,一个长度为1的对象数组即可。
设当前格子能获得的最大礼物价值为f(i, j), 要到达该位置,只有两种情况:
- 从该位置的左边来,即f(i, j-1)
- 从该位置的上边来,即f(i-1, j)
f(i, j)处的礼物价值设为gift(i, j)
那么到达f(i, j)处能收集到的最大礼物价值为
max[f(i, j- 1), f(i-1, j)]+gift[i, j]
可以发现,要知道当前格子能获得最大礼物价值,需要用到当前格子左边一个和上面一个格子的最大礼物价值和。所以从左上角开始,计算到达每一个格子能获得最大礼物价值是多少,并保存下这些结果。在后面求其他格子的最大礼物价值时会用到前面的结果。基于这个思路可写出如下代码。
/**
* 动态规划求解
* @param gifts
* @return
*/
public int getMaxValue2(int[][] gifts) {
if (gifts == null || gifts.length == 0) {
return 0;
}
int rows = gifts.length;
int cols = gifts[0].length;
int[][] max = new int[rows][cols];
for (int row = 0; row < rows; row++) {
for (int col = 0; col < cols; col++) {
int left = 0;
int up = 0;
if (row > 0) {
up = max[row - 1][col];
}
if (col > 0) {
left = max[row][col - 1];
}
max[row][col] = Math.max(up, left) + gifts[row][col];
}
}
return max[rows - 1][cols - 1];
}用到一个二维数组保存到达每一个格子时能获得的最大礼物价值。up和left分别是上面说的f(i-1, j)和f(i, j -1),循环完毕后,返回到达右下角处能获得最大礼物价值即可。
当前礼物的最大价值只依赖f(i-1, j)和f(i, j -1)这两个格子,因此只需要当前行i,第j列的前面几个格子,也就是f(i, 0)~f(i, j-1);以及i -1行的,第j列及其之后的几个格子,也就是f(i-1, j)~f(i-1, cols-1)
两部分加起来的个数刚好是棋盘的列数cols。所以只需要一个长度为cols的一维数组即可,优化如下。
/**
* 上述方法优化,用一维数组代替二维数组
* @param gifts
* @return
*/
public int betterGetMaxVal(int[][] gifts) {
if (gifts == null || gifts.length == 0) {
return 0;
}
int rows = gifts.length;
int cols = gifts[0].length;
int[] maxVal = new int[cols];
for (int row = 0; row < rows; row++) {
for (int col = 0; col < cols; col++) {
int left = 0;
int up = 0;
if (row > 0) up = maxVal[col];
if (col > 0) left = maxVal[col -1];
maxVal[col] = Math.max(up, left) + gifts[row][col];
}
}
return maxVal[cols-1];
}手动模拟一遍
- 功能测试(多行多列的矩阵;一行或者一列的矩阵;只有一个数字的矩阵)
- 特殊输入测试(指向矩阵数组的指针为null)
题目:请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长字符串的长度。假设字符串中只包含'a'-'z'的字符。
例如,在字符串“arabcacfr”中,最长的不含重复字符的子字符串是“acfr”,长度为4。
动态规划,定义$f(i)$表示以第i个字符为结尾的不含重复字符的子字符串长度。
如果第i个字符之前没有出现过,则$f(i) = f(i -1) +1$,比如‘abc',$f(0) = 1$是必然的,然后字符’b‘之前没有出现过,则$f(1) = f(0)+1$, 字符’c'之前没有出现过,那么$f(2) = f(1) +1$,每次计算都会用到上一次计算的结果。
如果第i个字符之前出现过呢?找到该字符上次出现的位置preIndex,当前位置i - preIndex就得到这两个重复字符之间的距离,设为d。此时有两种情况
- 如果
d <= f(i-1),说明当前重复字符必然在f(i-1)所对应的字符串中,比如’bdcefgc‘,当前字符c前面出现过了,preIndex为2,此时d = 6 -2 = 4,小于f(i -1) = 7 (bdcefg)我们只好丢弃前一次出现的字符c及其前面的所有字符,得到当前最长不含重复字符的子字符串为’efgc‘,即f(i) = 4, 多举几个例子就知道,应该让f(i) = d; - 如果
d > f(i-1), 这说明当前重复字符必然在f(i-1)所对应的字符串之前,比如erabcdabr当前字符r和索引1处的r重复,preIndex =1, i = 8,d = 7。而f(i -1) = 4 (cdab),此时直接加1即可,即f(i) = f(i-1) +1
根据这两种情况可写出代码如下:
public class LongestSubstring {
public int longestSubString(String string) {
int[] position = new int[26];
Arrays.fill(position, -1);
int p = 0;
int max = 0;
for (int i = 0; i < string.length(); i++) {
int pre = position[string.charAt(i) - 'a'];
if (pre == -1 || i - pre > p) {
p++;
} else {
p = i-pre;
}
position[string.charAt(i) - 'a'] = i;
if (max < p) {
max = p;
}
}
return max;
}
public static void main(String[] args) {
LongestSubstring longestSubstring = new LongestSubstring();
// int max1 = longestSubstring.longestSubString("bdcefgc");
int max2 = longestSubstring.longestSubString("erabcdabr");
// System.out.println(max1);
System.out.println(max2);
}
}- 功能测试(包含多个字符的字符串;只有一个字符的字符串;所有字符都唯一的字符串;所有字符都本周的字符串)。
- 特殊输入测试(空字符串)
题目:我们把只包含因子2,3和5的数称作丑数。求按从小到大的顺序的第1500个丑数。
例如,6,8都是丑数,但14不是,因为它包含因子7.习惯上我们抒1当作第一个丑数
根据丑数的定义,丑数应该是另一个丑数乘以2,3或者5的结果(1除外)。因此我们可以创建一个数组,里面的数字是排好序的丑数,每个丑数都是前面丑数乘以2,3或者5得到的.
根据丑数的定义,所有丑数都是2、3、5这三个因子的任意搭配的任意多次乘积,比如2x2,2x3, 2x2x3x5等等。那么从1开始,分别乘以2、3、5,得到2、3、5三个丑数,但是这并不是正确的排序,我们知道3、5之间还有个4也是丑数。1之后的下一个丑数,一定是2、3、5其中的一个,显然应该选三者中最小的2,现在丑数集合为{1, 2}且有序,刚才选走的2是1x2得到的,因此下一个和2相乘的丑数应该是1之后的数字2(丑数集合已经有序,直接选择下一个)。现在又得到三个候选的丑数4、3、5,再次选择三者中最小的3,得到当前丑数集合{1, 2, 3},刚被选走的3由1x3得到,因此下一个要和3相乘的按照丑数集合的顺序应该是2,然后又得到了三个候选的丑数4、6、5,选择最小的4.....不断重复,自始至终只和丑数打交道。
设定三个数t2、t3、t3专门用于分别和2、3、5相乘,某次选择中选走了ti,那么ti从丑数集合中选择下一个数,下次再和i相乘生成一个新的候选丑数,本次没有被选中的,下次继续参与比较。这样能保证下一个丑数一定在三个候选项中,且是三个候选项中最小的那个。
public class GetUglyNum {
public int getUglyNum(int num) {
if (num <= 0) {
return 0;
}
int[] res = new int[num];
res[0] = 1;
int t2 = 0;
int t3 = 0;
int t5 = 0;
for (int i = 1; i < num; i++) {
int m2 = res[t2] * 2;
int m3 = res[t3] * 3;
int m5 = res[t5] * 5;
res[i] = Math.min(m2, Math.min(m3, m5));
if (res[i] == m2) {
t2++;
}
if (res[i] == m3) {
t3++;
}
if (res[i] == m5) {
t5++;
}
}
return res[num - 1];
}
public static void main(String[] args) {
GetUglyNum getUglyNum = new GetUglyNum();
int res = getUglyNum.getUglyNum(7);
System.out.println(res);
}
}- 功能测试(输入2,3,4,5,6等)。
- 特殊输入测试(边界值1;无效输入0)。
- 性能测试(输入较大的数字,舅1500)
题目一:字符串中第一个只出现一次的字符
在字符串中找出第一个只出现一次的字符。如输入“abaccdeff”,则输出’b‘
public class FirstNotReoeatingChar {
public char firstNotRepeatingChar(String string) {
if (string == null || string.length() == 0) {
return '\0';
}
int count[] = new int[256];
for (int i = 0; i < string.length(); i++) {
count[string.charAt(i)]++;
}
for (int i = 0; i < string.length(); i++) {
if (count[string.charAt(i)] == 1) {
return string.charAt(i);
}
}
return '\0';
}
public static void main(String[] args) {
FirstNotReoeatingChar firstNotReoeatingChar = new FirstNotReoeatingChar();
char res1 = firstNotReoeatingChar.firstNotRepeatingChar(null);
System.out.println(res1);
char res2 = firstNotReoeatingChar.firstNotRepeatingChar("abaccdeff");
System.out.println(res2);
}
}请实现一个函数,用来找出字符流中第一个只出现一次的字符。
例如,当从字符流中只读出前两个字符“go”时,第一个只出现一次的字符是’g‘;当从该字符流中读出前6个字符“google”时,第一个只出现一次的字符是’l‘。
使用一个insert函数模拟从字符流中读到一个字符。这次统计表int[] occur = new int[256]记录的是字符出现的索引.
- 如果某个字符出现过,那么
occur[someChar] >= 0; - 对于没有出现过的字符,令
occur[someChar] = -1; - 如果某个字符第二次出现,令
occur[someChar] = -2。
要获得当前字符串中第一个只出现一次的,只需从所有occur[someChar] >= 0中结果中找出出现索引最小的那个字符即可。
public class AppearOnceInStream {
private int[] count = new int[256];
private int index = 0;
public AppearOnceInStream() {
Arrays.fill(count, -1);
}
public void insert(char c) {
if (count[c] == -1) {
count[c] = index;
} else if (count[c] >= 0) {
count[c] = -2;
}
index++;
}
public char appearOnceInStream() {
int min = Integer.MAX_VALUE;
char c = '\0';
for (int i = 0; i < count.length; i++) {
if (count[i] >= 0 && count[i] < min) {
min = count[i];
c = (char) i;
}
}
return c;
}
public static void main(String[] args) {
AppearOnceInStream appearOnceInStream = new AppearOnceInStream();
appearOnceInStream.insert('g');
appearOnceInStream.insert('o');
System.out.println(appearOnceInStream.appearOnceInStream());
appearOnceInStream.insert('o');
appearOnceInStream.insert('g');
appearOnceInStream.insert('l');
appearOnceInStream.insert('e');
System.out.println(appearOnceInStream.appearOnceInStream());
}
}- 功能测试(读入一个字符;读入多个字符;读入所有字符都是唯一的;读入的所有字符都是重复出现的)
- 特殊输入测试(诗篇0个字符)
题目:在数组中有两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
例如,在数组{7,5,6,4}中,一共存在5个逆序对,分别是(7,6),(7,5),(7,4),(6,4)和(5,4)
暴力法很直观,拿第一个数和之后的每个数比较,然后拿第二个数和之后的每个数比较.....需要两个for循环可得到结果,时间复杂度为$O(n^2)$
用数组的归并过程来分析这道题,归并排序就是自上而下地将数组分割成左右两半子数组,然后递归地将子数组不断分割下去,最后子数组的大小为1,对于大小为1的子数组没有排序和归并的必要,因此递归到此结束;之后自下而上地对这若干个子数组两两归并、四四归并......每次归并后左右子数组都分别有序,最后再将整个数组归并,因而整个数组也有序了。
现在分析一个简单的例子,对于数组{7, 5, 6, 4},先分成了两个子数组,左子数组{7, 5}和右子数组{6, 4},进而分成左子数组{7}和右子数组{5}....7大于5,所以这是一个逆序对,同样6大于4也是一个逆序对。现在得到两个逆序对了。然后开始两两归并,左子数组和右子数组现已分别排序,{5, 7}和 {4, 6},因为大的数在右边,所以考虑从右边开始比较。比如7大于6,那么7肯定也大于4,所以如果左边某个数p1比右边某个数p2大了,p1无需再和p2之前的所有数进行比较,这就减少了比较次数。那么在右子数组中比7小的有多少呢?多举几个例子就能发现通用的公式:**p2及其之前的元素个数减去左子数组的长度。**要求整个数组的逆序对总数,只需将每个子数组中的逆序对个数累加即可。
理解上述分析后,其实本题就可以直接使用归并排序,只是在左子数组中的某个元素大于右子数组某个元素时,多加一步——计算逆序对个数即可。
public class InversePairs {
public int inversePairs(int[] array) {
if (array == null) {
return 0;
}
int[] aux = new int[array.length];
return sort(array, aux, 0, array.length - 1);
}
private int sort(int[] array, int[] aux, int low, int high) {
if (high <= low) {
return 0;
}
int mid = low + (high - low) / 2;
int left = sort(array, aux, low, mid);
int right = sort(array, aux, mid+1, high);
int merged = merge(array, aux, low, mid, high);
return left + right + merged;
}
private int merge(int[] array, int[] aux, int low, int mid, int high) {
int count = 0;
int len = (high - low) / 2;
int i = mid;
int j = high;
for (int k = low; k <= high; k++) {
aux[k] = array[k];
}
for (int k = high; k >= low; k--) {
if (i < low) array[k] = aux[j--];
else if (j < mid + 1) array[k] = aux[i--];
else if (aux[i] > aux[j]) {
// 在归并排序的基础上,在这里求count
count += j - low - len;
array[k] = aux[i--];
} else array[k] = aux[j--];
}
return count;
}
public static void main(String[] args) {
InversePairs inversePairs = new InversePairs();
int[] array = {7, 5, 6, 4};
int a = inversePairs.inversePairs(array);
System.out.println(a);
}
}题目:输入两个链表,找出它们的第一个公共节点。
链表节点定义如下:
public class ListNode {
public int val;
public ListNode next = null;
public ListNode(int val) {
this.val = val;
}
}说到使用额外空间,使用Set可以轻松找出第一个公共结点。所谓公共结点其实就是完全一样的元素,而Set不能存入相同元素,当第一次添加元素失败时,该结点就是第一个公共结点了。
/**
* 方法1:两个辅助栈,从尾到头,找到最后一个相同的结点
* @param head1
* @param head2
* @return
*/
public ListNode findFirstCommonNode(ListNode head1, ListNode head2) {
if (head1 == null || head2 == null) {
return null;
}
Set<ListNode> set = new HashSet<>();
ListNode p = head1;
ListNode q = head2;
while (p != null) {
set.add(p);
p = p.next;
}
while (q != null) {
if (!set.add(q)) {
return q;
}
q = q.next;
}
return null;
}因为第一个公共结点及其之后的结点都相同,所以我们可以将两条链表的尾部对齐
,但是两条链表的长短可能不一样。这就需要长链表先走若干步,然后两条链表一起走,知道遇到一个相同结点,该结点就是第一个公共结点。具体长链表要先多少步,当然是长短链表长度之差。所有需先遍历一遍链表得到两个链表的长度。
public ListNode findFirstCommonNode2(ListNode head1, ListNode head2) {
if (head1 == null || head2 == null) {
return null;
}
ListNode p = head1;
ListNode q = head2;
int len1 = 0;
int len2 = 0;
while (p != null) {
len1++;
p = p.next;
}
while (q != null) {
len2++;
q = q.next;
}
p = head1;
q = head2;
if (len1 > len2) {
for (int i = 0; i < len1 - len2; i++) {
p = p.next;
}
} else if (len2 > len1) {
for (int i = 0; i < len2 - len1; i++) {
q = q.next;
}
}
while (p != q && p != null) {
p = p.next;
q = q.next;
}
if (p == q && p != null) {
return p;
}else
return null;
}
public static void main(String[] args) {
FindFirstCommonNode findFirstCommonNode = new FindFirstCommonNode();
ListNode l1 = new ListNode(1);
ListNode l2 = new ListNode(2);
ListNode l3 = new ListNode(3);
ListNode l4 = new ListNode(4);
ListNode l5 = new ListNode(5);
ListNode l6 = new ListNode(6);
ListNode l7 = new ListNode(7);
ListNode l8 = new ListNode(8);
l1.next = l5;
l5.next = l6;
l6.next = l7;
l7.next = l8;
l2.next = l3;
l3.next = l4;
l4.next = l5;
ListNode commonNode1 = findFirstCommonNode.findFirstCommonNode1(l1, l2);
ListNode commonNode2 = findFirstCommonNode.findFirstCommonNode2(l1, l2);
System.out.println(commonNode1.val);
System.out.println(commonNode2.val);
}统计一个数字在排序数组中出现的次数。
例如,输入排序数组{1,2,3,3,3,3,4,5}和烃字3.由于3在这个数组中出现了4次,因此输出4
public int getNumOfK(int[] array,int k) {
if (array == null || array.length == 0) {
return 0;
}
int first = getFirstOfK(array, k, 0, array.length - 1);
int last = getLastOfK(array, k, 0, array.length - 1);
if (first != -1 && last != -1) {
return last - first + 1;
}
return -1;
}
private int getLastOfK(int[] array, int k, int low, int high) {
while (low <= high) {
int mid = (low + high) / 2;
if (array[mid] > k) {
high = mid - 1;
} else if (array[mid] < k) {
low = mid + 1;
} else {
if (mid == array.length-1 || array[mid + 1] != k) {
return mid;
} else {
low = mid + 1;
}
}
}
return -1;
}
private int getFirstOfK(int[] array, int k, int low, int high) {
while (low <= high) {
int mid = (low + high) / 2;
if (array[mid] > k) {
high = mid - 1;
} else if (array[mid] < k) {
low = mid + 1;
} else {
if (mid == 0 || array[mid - 1] != k) {
return mid;
} else {
high = mid - 1;
}
}
}
return -1;
}注意到要查找的数组元素都是int型的,我们知道普通二分查找只需稍微改变下返回值(返回low),就能得到一个排名方法——在数组中比k小的数有多少个,即k在数组中排名多少。有个很聪明的思路就是,在数组中查找接近k的浮点数。
private int rank(int[] array, double k) {
int low = 0;
int high = array.length - 1;
while (low <= high) {
int mid = (high + low) / 2;
if (k > array[mid]) {
low = mid + 1;
} else if (k < array[mid]) {
high = mid - 1;
}
}
return low;
}
public int getNumberOfK2(int[] array, int k) {
if (array == null || array.length == 0) {
return 0;
}
return rank(array, k + 0.5) - rank(array, k - 0.5);
}
一个长度为n-1的递增排序数组中的所有数字都是唯一的,并覓每个数字都在范围0-n-1之内,在范围0-n-1内的n个数字中有且只有一个数字不在该数组中,请找出这个数字。
举个简单的例子来找到规律。比如数组长度为8,那么该数组中的数字都是0-8之间的,但是缺了一个数字,比如缺了4,则该数组为{0, 1, 2, 3, 5, 6, 7,8}
可以发现,缺失数字还没出现时,始终有该数字在数组中的下标等于该数,即array[i] == i,但是从5开始不再有这样的关系。对于5及其之后的元素有array[i] == i+1,但是5之前的3仍然有array[3] == 3, 可以看到这是一个分界线。此时返回5所在的下标4就是我们要的答案。
如果找到这个分界线呢?数组是有序的,仍然采用二分查找。当mid处满足array[mid] == mid,说明mid处及其之前的数都没有缺失,因此可以直接在mid右边数组查找;当array[mid] != mid说明mid处之前有元素丢失,此时再判断一下mid前的一个元素是否也有元素丢失,如果没有说明mid处是第一个值和下标不相等的元素,返回下标mid就是答案;如果mid处的前一个元素也有元素丢失,就继续缩小查找范围,在mid的左边数组继续查找即可。
根据上面的描述,写出如下代码:
public class FindTheLossNumber {
public int findTheLossNumber(int[] array) {
if (array == null || array.length == 0) {
return -1;
}
int low = 0;
int high = array.length - 1;
while (low <= high) {
int mid = (high + low) / 2;
if (array[mid] == mid) {
low = mid + 1;
} else {
if (mid == 0 || array[mid - 1] == mid - 1) {
return mid;
}
high = mid - 1;
}
}
if (low == array.length) return array.length;
// 无效的输入数组,如不是递增排序,或者有的数字超出了0~n-1的范围
return -1;
}
public static void main(String[] args) {
FindTheLossNumber f = new FindTheLossNumber();
int[] array1 = {0, 1, 2, 3, 5, 6, 7, 8};
int[] array2 = {1, 2, 3, 4, 5, 6, 7, 8};
int res1 = f.findTheLossNumber(array1);
int res2 = f.findTheLossNumber(array2);
System.out.println(res1);
System.out.println(res2);
}
}假设一个单调递增的数组里的每个元素都是整数并且是唯一的,请编程实现一个函数,找出数组中任意一个数值等于其下标的元素。
例如,在数组{-3,-1,1,3,5}中,数字3和它的下标相等。
public class FindValEqualsIndex {
public int findValEqualsIndex(int[] array) {
if (array == null || array.length == 0) {
return -1;
}
int high = array.length - 1;
int low = 0;
while (low <= high) {
int mid = (low + high) / 2;
if (array[mid] == mid) {
return mid;
} else if (mid > array[mid]) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return -1;
}
public static void main(String[] args) {
FindValEqualsIndex f = new FindValEqualsIndex();
int[] array = {-3, -1, 1, 3, 5};
int index = f.findValEqualsIndex(array);
System.out.println(index);
}
}题目:给定一棵二叉搜索树,请找出其中第k大的节点。
例如,在图中的二叉搜索树里,按节点数值大小顺序,第三大节点的值是4.
5
3 7
2 4 6 8
public class FindKthNode {
public TreeNode findKthNode(TreeNode root, int k) {
if (root == null || k <= 0) {
return null;
}
LinkedList<TreeNode> stack = new LinkedList<>();
TreeNode p;
int count = 0;
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
if (!stack.isEmpty()) {
p = stack.pop();
count++;
if (count == k) {
return p;
}
root = p.right;
}
}
return null;
}
public static void main(String[] args) {
FindKthNode f = new FindKthNode();
TreeNode r2 = new TreeNode(2);
TreeNode r3 = new TreeNode(3);
TreeNode r4 = new TreeNode(4);
TreeNode r5 = new TreeNode(5);
TreeNode r6 = new TreeNode(6);
TreeNode r7 = new TreeNode(7);
TreeNode r8 = new TreeNode(8);
r5.left = r3;
r5.right = r7;
r3.left = r2;
r3.right = r4;
r7.left = r6;
r7.right = r8;
TreeNode res1 = f.findKthNode(r5, 10);
System.out.println(res1.val);
}
}输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根,叶节点)形成树的一条路径,最长路径的长度为树的深度。
1
2 3
4 5 6
7
public int depth(TreeNode root) {
if (root == null) {
return 0;
}
int left = depth(root.left) ;
int right = depth(root.right) ;
return Math.max(left, right) + 1;
}求深度,其实就是求这棵二叉树有多少层。于是采用BFS的层序遍历。关键就是怎么知道什么时候处理完了二叉树的一层?我们来模拟一下:
就假设这是棵满二叉树吧,根结点先入队列,此时队列中结点个数为1,接着会弹出这唯一的根结点,同时入列两个结点,此时第一层处理完毕;
现在队列中结点个数为2,我们出列两次,4个结点又会入列,此时第二层处理完毕;
现在队列中结点个数为4,我们出列4次,8个结点又会入列,此时第三层处理完毕....
发现规律了吗?**每次要出列前,先得到队列中现有的结点个数,假设是m,那么就在循环内出列m次,随即跳出循环,这样就算处理完一行了。**跳出循环后只需要将深度自增,最后层序遍历完毕也就得到了二叉树的深度。
public int depth2(TreeNode root) {
if (root == null) {
return 0;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int depth = 0;
TreeNode p;
while (!queue.isEmpty()) {
int layerSize = queue.size();
for (int i = 0; i < layerSize; i++) {
p = queue.poll();
if (p.left != null) {
queue.offer(p.left);
}
if (p.right != null) {
queue.offer(p.right);
}
}
depth++;
}
return depth;
}输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左,右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
1
2 3
4 5 6
7
仍然是先求得左右子树的深度,如果做差不超过1,就正常返回深度;如果超过了1就说明这不是棵平衡二叉树了,于是不断返回-1,直到根结点。如果不是平衡二叉树,最后会得到该二叉树的深度为-1,所以只需判断一棵二叉树的深度是不是大于等于0即可。
public boolean isBalanced(TreeNode root) {
return depth3(root) >= 0;
}
private int depth3(TreeNode root) {
if (root == null) {
return 0;
}
int left = depth3(root.left);
int right= depth3(root.right);
return left >= 0 && right >= 0 && Math.abs(left - right) <= 1 ? Math.max(left, right) + 1 : -1;
}题目一:
一个整形数组里除两个数字之外,其他数字都出现了两次。请写程序找出为两个只出现一次数数字。
要求时间复杂度为O(n),空间复杂度为O(1)
例如输入数组{2, 4, 3, 6, 3, 2, 5, 5},只有4和6这两个数字只出现了一次,其他数字都出现了两次,因此输出4和6。
如果不考虑空间,用哈希表统计频率倒是很简单.....
好吧,没有思路。书中使用的是位运算。
先考虑简单的情况,如果数组中只有一个数字出现了一次而其他数都出现了两次。那么对数组中的每个数都做异或运算,因为两个相同的数每一位都相同,因此他们异或值为0,所有最后得到的结果就是那个只出现了一次的数。
现在只出现了一次的数有两个,只需要将这两个数分开,使得其中一个数在一个子数组中,另外一个数在另一个子数组中,再使用上面的方法即可。
由于有两个只出现了一次的数,对数组中所有数异或,得到的将是那两个只出现了一次的数的异或值。
就以上面的例子来说,最后会得到4和6的异或值,即100和110的异或值010(省略了前面29个0,因为int型是32位的),可以看到从右往左数的第2位是1,说明4和6在从右往左数的第2位不一样。在异或结果中找到第一个1的位置,假设是m(这说明那两个只出现了一次的数的第m位一个是1一个是0)。现在以第m位是不是1为标准将数组分成两部分,出现过两次的数一定会被分到同一个部分中,因为他们每一位都相同,第m位当然也相同;只出现过一次的两个数一定会被分到不同的部分中。
对这两部分分别异或,每一部分就得到了那么只出现了一次的数。
public class FindNumberAppearOnce {
public void findNum(int[] array, int[] num1, int[] num2) {
if (array == null || array.length < 2) {
return;
}
int temp = 0;
//将数组所有元素进行异或运算,最后得到的值 为两个不同元素的异或值,因为一个数异或它本身为0
for (int i = 0; i < array.length; i++) {
temp ^= array[i];
}
int index = findFirstOneIndex(temp);
num1[0] = num2[0] = 0;
for (int i = 0; i < array.length; i++) {
if (isBitOne(array[i], index)) {
num1[0] ^= array[i];
} else {
num2[0] ^= array[i];
}
}
}
/**
* 找到第1个为1的位置
* @param n
* @return
*/
private int findFirstOneIndex(int n) {
if (n == 0) {
return 0;
}
int count = 0;
while ((n & 1) != 1) {
n = n >> 1;
count++;
}
return count;
}
/**
* 判断该位 是否为1
* @param n
* @param index
* @return
*/
private boolean isBitOne(int n, int index) {
n = n >> index;
if ((n & 1) == 1) {
return true;
}
return false;
}
public static void main(String[] args) {
FindNumberAppearOnce f = new FindNumberAppearOnce();
int[] num1 = {0};
int[] num2 = {0};
int[] array = {2, 4, 3, 6, 3, 2, 5, 5};
f.findNum(array, num1, num2);
System.out.println(Arrays.toString(num1) + "\n" +
Arrays.toString(num2));
}
}在一个数组中除一个数字只出现一次之外,其他数字都出现了三次。请找出那个只出现一次的数字。
使用排序需要O(nlgn)的时间,使用哈希表需要O(n)的空间。有没有更好的?
一个int型有32位,每一位不是0就是1。对于三个相同的数,统计每一位出现的频率,那么每一位的频率和一定能被3整除,也就是说频率和不是3就是0。如果有多组三个相同的数,统计的结果也是类似:频率和不是0就是3的倍数。
现在其中混进了一个只出现一次的数,没关系也统计到频率和中。如果第n位的频率和还是3的倍数,说明只出现一次的这个数第n位是0;如果不能被3整除了,说明只出现一次的这个数第n位是1。由此可以确定这个只出现一次的数的二进制表示,想得到十进制还不简单吗。
public int findOnceNum(int[] array) {
if (array == null || array.length == 0) {
throw new RuntimeException("Input Error");
}
int[] res = new int[32];
int bit = 1;
for (int i = 31; i >= 0; i--) {
for (int num : array) {
//第i位不为1
if ((num & bit) != 0) {
res[i]++;
}
}
bit = bit << 1;
}
int num = 0;
// 转换成十进制时,从最高位开始,从由左至右第一个不为0的位开始
for (int i = 0; i <32; i++) {
num = num << 1;
num += res[i] % 3;
}
return num;
}
public static void main(String[] args) {
FindOnceNum f = new FindOnceNum();
int[] array = {3, 3, 3, 6};
int res = f.findOnceNum(array);
System.out.println(res);
}要注意的一点是,统计每一位的频率时,是从最低位开始的,bitSum[31]存的是最低位的频率和,而bitSum[0]存的是最高位的频率和,这和人从左往右的阅读习惯一致。从二进制转换成十进制时,则是从最高位开始的,从由左至右第一个不为0的位开始累加,最后得到该数的十进制表示,返回即可。
该方法只需要O(n)的时间,空间复杂度为O(1)。
输入一个递增排序的数组和一个数字s,在数组中查找两个数,使得它们的和正好是s。如果有多对数字的和等于s,则输出任意一对即可。
例如,输入数组{1,2,4,7,11,15}和数字15.由于4+11=15,因此输出4和11.
public void findNumberWithSum(int[] array, int num, int[] num1, int[] num2) {
if (array == null || array.length == 0) {
return;
}
int low = 0;
int high = array.length - 1;
while (low <= high) {
if (array[low] + array[high] == num) {
num1[0] = array[low];
num2[0] = array[high];
return;
} else if (array[low] + array[high] > num) {
high--;
} else {
low++;
}
}
return;
}输入一个正数s,打印出所有和为s的连续正数序列(至少含有两个数)。
例如,输入15,由于1+2+3+4+5=4+5+6=7+8=15,所以打印出3个连续序列1-5,4-6和7-8.
public class FindContinuousSequence {
public ArrayList<ArrayList<Integer>> findContinuousSequence(int sum) {
ArrayList<ArrayList<Integer>> res = new ArrayList<>();
if (sum < 1) {
return res;
}
int mid = (sum + 1) / 2;
int low = 1;
int high = 2;
int curSum = 0;
ArrayList<Integer> temp = new ArrayList<>();
while (high <= mid) {
curSum = (low + high) * (high - low + 1) / 2;
if (curSum == sum) {
for (int i = low; i <= high; i++) {
temp.add(i);
}
res.add(new ArrayList<>(temp));
temp.clear();
low++;
high = low + 1;
} else if (curSum < sum) {
high++;
} else {
low++;
}
}
return res;
}
public static void main(String[] args) {
FindContinuousSequence f = new FindContinuousSequence();
ArrayList<ArrayList<Integer>> res = f.findContinuousSequence(9);
System.out.println(res);
}
}输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。为简单起见,标点符号和就能字母一样处理。
例如,输入字符串“I am a student.”则输出"student. a am I".
public class ReverseSentence {
public String reverse(String sentence) {
if (sentence == null || sentence.trim().equals("")) {
return "";
}
String[] words = sentence.split("\\s+");
StringBuilder sb = new StringBuilder();
for (int i = words.length - 1; i >= 0; i--) {
sb.append(words[i]);
if (i > 0) {
sb.append(" ");
}
}
return sb.toString();
}
public static void main(String[] args) {
ReverseSentence rs = new ReverseSentence();
String re = rs.reverse("I am a student.");
System.out.println(re);
}
}字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。
比如,输入字符串“abcdefg”和数字2,该函数将返回左旋转两位得到的结果"cdrfgab".
举个简单的例子"hello world",按照上题的要求,会得到"world hello". 而在此题中,假如要求将前五个字符左旋转,会得到" worldhello"(注意w前哟一个空格),是不是接近了。
所以本题可以延续上题的思路,不过这次先局部翻转再整体反转。如字符串"abcdefg"要求左旋转前两个字符,先反转ab和cdefg得到bagfedc,然后反转这个字符串得到cdefgab即是正确答案。
public class RotateString {
public String rotateString(String str, int n) {
if (str == null || str.length() == 0 || str.length() < n) {
return "";
}
char[] chars = str.toCharArray();
reverse(chars, 0, n - 1);
reverse(chars, n, str.length() - 1);
reverse(chars, 0, str.length() - 1);
return new String(chars);
}
private void reverse(char[] chars, int low, int high) {
while (low <= high) {
char c = chars[high];
chars[high] = chars[low];
chars[low] = c;
low++;
high--;
}
}
public static void main(String[] args) {
RotateString rs = new RotateString();
String res = rs.rotateString("abcdefg", 2);
System.out.println(res);
}
}给定一个数组和滑动窗口的大小,请找出所有滑动窗口里的最大值。
例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,它们的嗫大值分别为{4,4,6,6,6,5}
就以题目中的例子来模拟找出窗口中的最大值的过程。先存入3个元素,于是优先队列中有{2, 3, 4},使用peek方法可以以O(1)的时间得到最大值,之后删除队列头的元素2,同时入列下一个元素,此时队列中有{3, 4, 2},再调用peek方法得到最大值,然后删除队列头的3,下一个元素入列......不断重复进行此操作,直到最后队列中只有两个元素为止。
/**
* 使用优先队列(最大堆)
* @param array
* @param size
* @return
*/
public ArrayList<Integer> maxInWindow(int[] array, int size) {
ArrayList<Integer> res = new ArrayList<>();
if (array == null || array.length < size || size <= 0) {
return res;
}
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
int j = 0;
for (int i = 0; i < array.length; i++) {
maxHeap.offer(array[i]);
if (maxHeap.size() >= size) {
res.add(maxHeap.peek());
maxHeap.remove(array[j++]);
}
}
return res;
}这种思路只将有可能成为滑动窗口中的最大值的元素入列。
使用双端队列,队列头永远存放当前滑动窗口的最大值,而队列尾存放候选最大值,即当队列头的最大值弹出后成为新的最大值的那些元素。以题目中的例子模拟下该思路。
一开始2进入队列,然后3进入队列,因为3比2大,所以2不可能是滑动窗口的最大值。因此先将2从队列中弹出,然后3入列;接下来4入列也类似:将3弹出,4入列,目前队列中只有一个元素,且滑动窗口中已经有三个数字了,所以此时窗口中的最大值是位于队列头的4。
接下来2入列,虽然比4小,但是不知道什么时候4将会位于滑动窗口之外,所以这个2还是有一定可能成为窗口中的最大值的,应该将其入列,注意应该排在队列的尾部,因为队列头始终是当前窗口的最大值。由于队列头还是4,所以此时窗口中的最大值还是4。
然后6入列,队列中的4和2都不可能成为窗口中的最大值了,因此应该先从队列中弹出4和2然后再将6入列....后面的分析也大同小异。
......
再看最后一个元素1,它入列前,队列中有6和5,且6位于队列头是窗口中的最大值,按照之前的做法,应该将1入列,但是窗口的大小为3,此时队列头的6已经在窗口之外了,所以要讲6从队列中弹出,那么此时队列中还剩下5和1且5位于队列头,所以最后一个窗口中的最大值是5。**那么如何判断某个元素还在不在窗口内呢?我们应该在往队列中存元素的下标而不是元素本身。**若当前正访问的元素的下标与窗口最大值的下标(即队列头元素的下标)超过了窗口的宽度,就应该从队列头删除这个在滑动窗口之外的最大值。
总之就是:
- 即将要入列的的元素比队列中哪些元素大或者相等,就将那些元素先从队列中删除,然后再入列新元素;
- 队列头的最大值如果位于滑动窗口之外,则需要将队列头的最大值从队列中删除;
- 当前下标加上1(因为下标从0开始计)等于窗口宽度的时候就可以开始统计滑动窗口的最大值了
基于以上三点可写出下面的代码
/**
* 使用双端队列,存入数组下标
* @param array
* @param size
* @return
*/
public ArrayList<Integer> maxInWindow2(int[] array, int size) {
ArrayList<Integer> res = new ArrayList<>();
if (array == null || array.length < size || size <= 0) {
return res;
}
Deque<Integer> deque = new LinkedList<>();
for (int i = 0; i < array.length; i++) {
while (!deque.isEmpty() && array[i] >= array[deque.peekLast()]) {
deque.pollLast();
}
if (!deque.isEmpty() && i - deque.peekFirst() >= size) {
deque.pollFirst();
}
deque.offerLast(i);
if (i + 1 >= size) {
res.add(array[deque.peekFirst()]);
}
}
return res;
}请定义一个队列并实现函数max得到队列里的最大值,要求函数max,push_back和oio_front的时间复杂度都是O(1)
此题和面试题30“包含min的栈”同一个思路。
一个dataQueue正常入列、出列元素,为了以O(1)的时间获取当前队列的最大值,需要使用一个maxQueue存放当前队列中最大值。具体来说就是,如果即将要存入的元素比当前最大值还大,那么存入这个元素;否则再次存入当前最大值。
public class MaxQueue {
private Deque<Integer> maxQueue = new LinkedList<>();
private Deque<Integer> dataQueue = new LinkedList<>();
public void offer(int n) {
dataQueue.offerLast(n);
//即将要存入的元素比当前队列最大值还大,存入该元素
if (maxQueue.isEmpty() || n > maxQueue.peekFirst()) {
maxQueue.offerFirst(n);
} else {
//即将要存入和元素不超过当前队列最大值,再将最大值存入一次
maxQueue.offerFirst(maxQueue.peekFirst());
}
}
public void poll() {
if (dataQueue.isEmpty()) {
throw new RuntimeException("队列已空");
}
dataQueue.pollFirst();
maxQueue.pollFirst();
}
public int max() {
if (maxQueue.isEmpty()) {
throw new RuntimeException("队列已空");
}
return maxQueue.peekFirst();
}还是上面的例子{2, 3, 4, 2, 6, 2, 5},分析随着各个元素入列dataQueue和maxQueue的情况。
| 操作 | dataQueue | maxQueue | max |
|---|---|---|---|
| 2入列 | 2 | 2 | 2 |
| 3入列 | 2, 3 | 3, 2 | 3 |
| 4入列 | 2, 3, 4 | 4, 3, 2 | 4 |
| 2入列 | 2, 3, 4, 2 | 4, 4, 3, 2 | 4 |
| 6入列 | 2, 3, 4, 2, 6 | 6, 4, 4, 3, 2 | 6 |
| 2入列 | 2, 3, 4, 2, 6, 2 | 6, 6, 4, 4, 3, 2 | 6 |
| 5入列 | 2, 3, 4, 2, 6, 2, 5 | 6, 6, 6, 4, 4, 3, 2 | 6 |
出列的话两个队列同时出列一个元素,保证了maxQueue的队列头元素始终是dataQueue的当前最大值。
题目:把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入m,打印出s的所有可能的值出现的概率。
n个骰子,我们可以投掷n次,累加每次掷出的点数即可。因此要求出n个骰子的点数和,可以从n个骰子先取出一个投掷,这一个骰子只可能出现1-6中的某一个数,我们需要计算的是1-6每个点数与剩下n -1个骰子的点数和;接下来进行第二次投掷,现在骰子堆中还有n - 1个骰子,对于这n -1个骰子,继续从中选一个出来投掷,并在上次掷出的点数上累加...这显然是个递归过程。不断投掷,直到最后一个骰子也被投掷并累加点数,之后骰子数为0,也达到了递归终止的条件。
一个骰子可能出现的点数和是1-6,两个骰子可能出现的点数和为2-12,三个骰子可能出现的点数和为3-18,因此n个骰子可能出现的点数为n-6n。可以用一个大小为6n - n + 1的数组存放每个可能的点数和出现的频率,比如该数组下标0处存放的是点数和为n的出现次数;而下标6n -n处存放的是点数和6n的出现次数。n个骰子,每次投掷都有6种情况,因此总的点数和情况为$6 ^ n$种。要求某个点数和出现的概率,用该点数和出现的频次除以$6 ^ n$即可。
public void printProbability(int n) {
if (n < 1) {
return;
}
int maxVal = 6 * n;
int[] p = new int[maxVal - n + 1];
getProbabilities(n, n, 0, p);
int total = (int) Math.pow(6, n);
for (int i = n; i <= maxVal; i++) {
System.out.println("s=" + i + ": " + p[i - n] + "/" + total);
}
}
private void getProbabilities(int n, int cur, int sum, int[] p) {
if (cur == 0) {
p[sum - n]++;
} else {
for (int i = 1; i <= 6; i++) {
getProbabilities(n, cur-1, sum+i, p);
}
}
}题目:从扑克牌中随机抽5张牌,判断是不是一个顺子,即为5张牌是不是连续的。2-10为数字本身,A为1,J为11.Q为12,K为13,而大,小王可以看成任意数字
正常的顺子比如23456,假如含有大小王呢?03467也能构成顺子,虽然4和6中间有一个间隔,但是因为存在一张大小王,刚好可以让它成为5而填补上4和6之间的间隔。再假设是00367也能构成顺子,3和6之间有两个间隔但是刚好有两个王可以填补。更特殊的02345, 00234, 这种没有本身间隔的牌组合,因为大小王可以作任何数字,显然也构成顺子。
接下来看不能构成顺子的例子,34578,以及03678或者00378,可以发现当王的个数比间隔数少的话就不能构成顺子,反之如果王的个数大于等于间隔数,就能构成顺子。
要计算相邻两张牌的间隔,需要牌组合已经有序,因此第一步就要对五张牌排序。因此这种思路需要O(nlgn)的时间。
基于上述思路写出如下代码:
public class PlayCard {
public boolean isContinue(int[] array) {
if (array == null || array.length != 5) {
return false;
}
Arrays.sort(array);
int joker = 0;
//统计0的个数
for (int i = 0; i < array.length; i++) {
if (array[i] == 0) {
joker++;
}
}
int gap = 0;
//统计gap
for (int i = array.length - 1; i > joker; i--) {
if (array[i] == array[i - 1]) {
return false;
}
gap += array[i] - array[i - 1] - 1;
}
return gap <= joker;
}
public static void main(String[] args) {
PlayCard playCard = new PlayCard();
int[] array = {0, 2, 5, 6, 7};
boolean b = playCard.isContinue(array);
System.out.println(b);
}
}五张牌组合成的顺子,都有哪些共性呢?如果牌中没有大小王,那么23456, 56789等这样的组合才是顺子;即五张牌中最大值和最小值的差始终是4,且任意两张牌不重复;现在假设有大小王(用0表示),02345、03467、00367都是顺子,但03678、00378不是顺子。发现大小王可多次出现,因此五张牌中0可以重复出现。除开0之外,其他牌不能重复出现且最大值与最小值的差小于5。综合以上两种情况,要想构成顺子,需要满足以下条件:
- 除开0之外,其他任意牌不得重复出现
- 除开0之外的其他牌,最大值和最小值的差要小于5
基于以上两条规则,可写出如下代码:
/**
* 利用顺子本身规律
* @param array
* @return
*/
public boolean isContinue2(int[] array) {
if (array == null || array.length != 5) {
return false;
}
int[] count = new int[14];
int max = -1;
int min = 14;
for (int number : array) {
count[number]++;
//对除了0之外的其他数将运算最大值最小值
if (number != 0) {
if (count[number] > 1) {
return false;
}
if (number > max) {
max = number;
}
if (number < min) {
min = number;
}
}
//如果没有0,最大最小值之差为4,有0还能凑成顺子的,差值小于4;大于4肯定不能凑成顺子
}
return max - min < 5;
}题目:0,1,...,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。
比较直观的思路就是模拟游戏的过程,题目中说到圆圈而且要经常删除元素,因此容易想到用环形链表,但是Java内置的数据结构中没有环形链表,那么只好当遍历到链表末尾时转到链表头部。
举个简单的例子{0, 1, 2, 3, 4}和m = 3。从0开始第一个被删除的将是2,然后圆圈里剩下{0,1, 3, 4},接下来从3开始计数,那么下一个被删除的将是0(注意这里到链表末尾所以转到了链表头),然后圆圈里剩下{1, 3, 4}从1开始计数下一个被删除的是4,现在圆圈里剩下{1, 3},从下一个元素1开始计数,将被删除的元素是1,最后圆圈只剩下3了。
遍历到链表尾部需要转到链表头部,对于这个操作,可以设置一个整数p,表示链表中某元素的下标,每走一步p自增,走到链表尾部时(即p和链表长度相等),将该指针值置为0表示回到链表头部;同样如果删除的正好是链表的最后一个元素,下一个开始计数的应该是链表头部,所以这种情况下也要将p置为0。
public int lastIncircle(int n,int m) {
if (m <= 0 || n <= 0) {
return -1;
}
LinkedList<Integer> list = new LinkedList<>();
for (int i = 0; i < n; i++) {
list.add(i);
}
int index = 0;
while (list.size() > 1) {
index = (m - 1 + index) % n;
list.remove(index);
n--;
}
return list.get(0);
}令$f(n, m)$为n个数字0, 1, ...n -1中删除第m个数字后,最后剩下的那个数字。
要删除第m个数字,因为从0开始计数,所以计数到m-1,在这n个数中,第一个被删除的是(m -1) % n,不妨设k = (m -1) % n。删除k之后,剩下0,1,...k-1,k+1,...n -1下一个要从k+1开始计数。
既然从k+1开始计数,相当于把k+1放在最前面,k+1,...n-1,0,1,k-1由于此时打乱了数字排列的规律,该函数已不再是$f(n-1, m)$了,不妨表示为$f'(n -1, m)$
现在把k + 1认为是0,k+2认为是1,以此类推,因为刚删除了一个元素,所以只有n-1个元素了,映射表如下
0 -> k+1
1 -> k+2
...
n-k-2 -> n-1
n-k-1 -> 0
n-k -> 1
n-2 -> k-1
如果用x’表示重排后新序列中的元素(上表中箭头右边的数),x表示x'被当作的数字,那么有x' = (x + k + 1) % n ,所以下式也成立
f'(n -1, m) = [f(n-1, m) + k + 1] % n
还有,最初序列最后剩下的数字$f(n,m)$和删除一个数字后的序列最后剩下的数字时同一个,因此有$f(n,m)=f'(n-1, m)$
综合以上各式,再代入k = (m-1) % n
f(n, m) = [f(n-1, m) + m] % n ,n > 1
且恒有f(1, m) = 0, n = 1,因为如果只有一个数(这个数是0),那么无需删除,最后一个剩下的数就是它。既然知道了$f(1, m)$根据上式就能求出$f(2, m)$,以此类推,只需一个循环就能求出$f(n, m)$
/**
* 数学规律:约瑟夫环问题
*/
public int lastNumInCycle2(int n, int m) {
if (n <= 0 || m <= 0) return -1;
int f = 0;
for (int i = 2; i <= n; i++) {
f = (f + m) % i;
}
return f;
}题目:假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖该股票一次可能获得的最大利润是多少?
例如,一只股票在某些时间节点的价格为{9,11,8,5,7,12,16,14}.如果我们能在价格为5的时候买入并在价格为16时卖出,则能收获最大的利润11.
咋一看好像只要求出数组中的最大/最小值就完事了,但是数组中的值是按照时间顺序排列的,这就是说假如数组中最小值在最大值之后,它们的差值不会是股票的最大利润。因此我们要求的是数组中排在后面的数(售出价格)与排在前面的数(购入价格)的最大差值。
暴力法是$O(n^2)$的复杂度,就不考虑了。我们力求在一次循环中就求出最大差值。假设当前访问的数组下标是i,只需记住当前下标之前所有元素中的最小值即可,用一个int型的变量min维护这个最小值,每次用当前数字和min作差,差值用maxDiff保存,遍历一遍数组即可得出最大的差值。
public int maxProfit(int[] array) {
if (array == null || array.length == 0) {
return -1;
}
int minPrice = array[0];
int maxProfit = Integer.MIN_VALUE;
for (int i = 1; i < array.length; i++) {
if (array[i] - minPrice > maxProfit) {
maxProfit = array[i] - minPrice;
}
if (array[i] < minPrice) {
minPrice = array[i];
}
}
return maxProfit;
}题目:求1+2+..+n,要求不能使用乘除法,for,while,if,else,switch,case等关键字及条件判断语句(A?B:C)
使用逻辑与的短路特性可以构造出一个条件语句出来,逻辑与的短路特性是指:如果前面的条件已经不成立,后面的条件不会被判断了。上面的递归中当n == 1时就终止递归了直接返回n(也就是1);所以只需将上面程序改一改:
public int sum(int n) {
int sum = n;
boolean b = n > 0 && (sum+=sum(n - 1)) > 0;
return sum;
}
等差数列求和公式大家都很熟悉,如下: $$ S_n = n(n+1)/2 $$
题目中说了不能用乘除法,但是没说不能用加法和位运算,所以上式稍作变形可以得到
$$
S_n = (n^2 + n) >> 1
$$
其中>> 1表示右移一位,其实就是除以2。那这下就简单多了,哈哈。
public int sum2(int n) {
return (int)(Math.pow(n, 2) + n) >> 1;
}题目:写一个函数,求两个整数之和,要求在函数体愉产处使用”+“,”-“,”x“,”/“四则运算符号
不能用四则运算,自然容易想到用位运算。但如何使用位运算作加法呢?先来分析十进制是如何作加法的。比如要18 + 6
1 8
+ 0 6
——————
1 4
+ 1 0
——————
2 4
1) 个位和个位相加,十位与十位相加,但不进位;
2) 6 + 8产生一位进位得到10,1 + 0不产生进位;
3) 不进位的和14 + 个位的进位10 = 24。
没有进位了,计算停止。
可以看到十进制作加法可以细分为以上三步。那么对于二进制的加法呢?18的二进制是10010,6的二进制是110
10010
+ 00110
————————
10100
+ 00100 (还有进位,继续计算)
————————
10000
+ 01000 (没有进位,停止计算)
————————
11000
11000正好是24的十进制表示。换成二进制作加法,原理一样。关键是:如果还有进位,要不断累加,直到没有进位,此时计算才停止。
对于二进制,不进位的的加法就是异或运算,计算进位只需将两个数相与并向左移一位(也就是进位)。
接下来写代码就不难了。
public class Add {
public int add(int a, int b) {
//b!=0 说明还有进位需要相加
while (b != 0) {
int sum = a ^ b;
int carry = (a & b) << 1;
a = sum;
b = carry;
}
return a;
}
public static void main(String[] args) {
Add add = new Add();
int sum = add.add(15, 8);
System.out.println(sum);
}
}一般写个swap方法,需要引入第三个变量。如下
public int swap(int a, int b) {
int temp = a;
a = b;
b = temp;
}如果要交换的数据类型是int型的数字,如何不使用新的变量,交换两个变量的值?使用如下的运算即可完成。
a = a + b;
b = a - b;
a = a - b;
或者
a = a ^ b;
b = a ^ b;
a = a ^ b;在纸上推导下就能验证上面式子的正确性。
题目:给定一个数组A[0,1,...n-1],请构建一个数组B[0,1,...,n-1],其中B中元素B[i]=A[0]xA[1]x...xA[i-1]xA[i+1]...A[n-1]。不能使用除法。
如果可以使用除法,直接除以A[i]就可以得到B[i],但是现在要求了不能使用除法,只好另辟蹊径了。
一种方法是剔除A[i]进行连乘计算B[i],计算一次的时间是
有没有$O(n)$的算法呢。
注意到B[i]是 除了A[i] 之外A[0]到A[n - 1]的连乘。那么可以考虑从A[i]处将乘积分成两部分。C[i] = A[0]*A[1]*...*A[i - 1],D[i] = A[i + 1]*...A[n - 2]*A[n -1];
而C[i] = C[i -1]*A[i -1],D[i] = D[i + 1]*A[i + 1]
根据这些关系计算出C[i]和D[i],最后求得B[i] = C[i] * D[i]即可。
如上图,表中每一行的第一个数就是其后每个数字连乘,没有被乘上的数字A[i]就用1表示了,反正乘积不变。显然C[0] = 1,我们可以用C[i] = C[i -1]*A[i -1]计算出对角线左边的三角中各个A[i]的值;显然D[n -1] = 1,再D[i] = D[i + 1]*A[i + 1]计算对角线右边的三角中各个A[i]的值,然后将两者相乘就能得到B[i]。
public int[] multiply(int[] A) {
if (A == null || A.length < 2) {
return null;
}
int len = A.length;
int[] B = new int[len];
B[0] = 1;
for (int i = 1; i < len; i++) {
B[i] = B[i - 1] * A[i - 1];
}
int d = 1;
for (int i = len - 2; i >= 0; i--) {
d = d * A[i + 1];
B[i] *= d;
}
return B;
}
public static void main(String[] args) {
Multiply m = new Multiply();
int[] array = {1, 2, 3, 4};
int[] b = m.multiply(array);
System.out.println(Arrays.toString(b));
}将一个字符串转换成一个整数,要求不能使用字符串转换整数的库函数。 数值为0或者字符串不是一个合法的数值则返回0
我们知道Java内置了Integer.parseInt(String s),直接调用即可。如果要自己写呢,你可能很快想出如下代码
public class StrToInt {
public static boolean valid;
public long strToInt(String str) {
if (str == null || str.length() == 0) {
valid = false;
return 0;
}
//这里为long
long num = 0;
boolean isNegative = false;
for (int i = 0; i < str.length(); i++) {
if (i == 0 && (str.charAt(i) == '+' || str.charAt(i) == '-')) {
if (str.charAt(i) == '+') {
isNegative = false;
}
if (str.charAt(i) == '-') {
isNegative = true;
}
continue;
}
if (str.charAt(i) > '9' || str.charAt(i) < '0') {
valid = false;
return 0;
}
int flag = isNegative ? -1 : 1;
num = num * 10 + flag*(str.charAt(i) - '0');
if (isNegative && num < Integer.MIN_VALUE || !isNegative && num > Integer.MAX_VALUE) {
valid = false;
return 0;
}
}
valid = true;
return num;
}
public static void main(String[] args) {
StrToInt s = new StrToInt();
System.out.println(s.strToInt("12"));
System.out.println(s.strToInt("-12"));
System.out.println(s.strToInt("+12"));
System.out.println(s.strToInt("+")+ " "+ StrToInt.valid);
System.out.println(s.strToInt("0")+ " "+ StrToInt.valid);
System.out.println(s.strToInt("12345678901112")+ " "+ StrToInt.valid);
}
}这道题说得很含糊,仅仅告诉了*一棵树,*那这棵树是二叉树吗?再具体点,它是二叉查找树吗?我们来一一讨论这这几种情况。
二叉查找树的特点是:任意父节点都大于其左子树的所有结点值,且都小于其右子树的所有结点值。两个结点的公共祖先一定是大于其中较小的那个且小于其中较大的那个,而从根结点开始从上到下遇到的第一个位于两个输入结点值之间的结点就是最低的公共祖先。
于是我们可以这么做:从根结点开始,和两个输入结点的值比较,如果当前结点比两个输入都小,那么最低公共祖先一定在当前结点的右子树中,所以下步遍历右子树;如果当前结点比两个输入都大,那么最低公共祖先一定在当前结点的左子树中,所以遍历左子树......直到找到第一个位于两个输入结点值之间的结点就是最低的公共祖先。
/**
* 二叉查找树
* @param root
* @param a
* @param b
* @return
*/
public TreeNode findLastSame(TreeNode root, TreeNode a, TreeNode b) {
if (root == null || a== null || b== null) {
return null;
}
TreeNode p = root;
while (p != null) {
if (p.val < a.val && p.val < b.val) {
p = p.right;
}
if (p.val > a.val && p.val > b.val) {
p = p.left;
}
if ((p.val > a.val && p.val < b.val) || (p.val < a.val && p.val > b.val)) {
return p;
}
}
return null;
}如果这棵树只是一颗普通的树,但是它拥有指向父结点的指针,该如何求最低公共祖先呢。
这个问题就更简单了,拥有指向父结点的话,这棵树从下往上看,就是若干条链表汇集在根结点处。我们要找的就是这两个结点的第一个公共结点。
之前刚好做过一道题面试题52就是求两个链表的第一个公共结点,直接把代码拿过来就行。
此处省略代码
这道题再加大难度,如果没有指向父结点的指针呢?是否还能转换成两个链表的第一个公共结点来解决?
想办法创造链表。两个输入结点如果在树中存在,那么从根结点开始向下的某条路径中必然包含这个结点,使用两个链表分别保存包含这两个结点的路径。这样就可以把问题转换成求两个链表的第一个公共结点了。
public class LastSameInCommonTree {
public CommonTreeNode findLastSame(CommonTreeNode root, CommonTreeNode a, CommonTreeNode b) {
if (root == null || a == null || b == null) {
return null;
}
LinkedList<CommonTreeNode> path1 = new LinkedList<>();
LinkedList<CommonTreeNode> path2 = new LinkedList<>();
collectNode(root, a, path1);
collectNode(root, b, path2);
CommonTreeNode node = getLastSameNode(path1, path2);
return node;
}
private boolean collectNode(CommonTreeNode root, CommonTreeNode a, LinkedList<CommonTreeNode> path) {
path.add(root);
if (root == a) {
return true;
}
for (CommonTreeNode p : root.children) {
if (collectNode(p, a, path)) {
return true;
}
}
path.remove(root);
return false;
}
private CommonTreeNode getLastSameNode(LinkedList<CommonTreeNode> path1, LinkedList<CommonTreeNode> path2) {
CommonTreeNode common = null;
while (!path1.isEmpty() && !path2.isEmpty()) {
if (path1.peek() == path2.removeFirst()) {
common = path1.removeFirst();
}
}
return common;
}
public static void main(String[] args) {
CommonTreeNode a = new CommonTreeNode("A");
CommonTreeNode b = new CommonTreeNode("B");
CommonTreeNode c = new CommonTreeNode("C");
CommonTreeNode d = new CommonTreeNode("D");
CommonTreeNode e = new CommonTreeNode("E");
CommonTreeNode f = new CommonTreeNode("F");
CommonTreeNode g = new CommonTreeNode("G");
a.children.add(b);
a.children.add(c);
a.children.add(d);
b.children.add(e);
b.children.add(f);
c.children.add(g);
LastSameInCommonTree l = new LastSameInCommonTree();
LinkedList<CommonTreeNode> path1 = new LinkedList<>();
LinkedList<CommonTreeNode> path2 = new LinkedList<>();
System.out.println(l.findLastSame(a, e, g).val);
System.out.println(l.findLastSame(a, e, f).val);
}
}上面代码中,路径是从根结点向下的,所以两个链表前面的结点都是相同的,这样就把两个链表的第一个公共结点问题转换成了两个链表的最后一个相等的结点,这两个命题是等价的。
得到两条路径需要遍历树两次,每次都是$O(n)$的时间,而每条路径需要的空间在平均情况下是$O(\lg n)$,最差情况下(树退化成链表)是$O(n)$
有N个孩子站成一排,每个孩子有一个分值。给这些孩子派发糖果,需要满足如下需求:
1、每个孩子至少分到一个糖果
2、分值更高的孩子比他相邻位的孩子获得更多的糖果
求至少需要分发多少糖果?
思路:
- 从左到右处理递增序列,分数更高的孩子获得更多的糖果
- 从右到左处理递增序列(即从左到右的递减序列),分数更高的孩子获得更多的糖果,两个递增序列重复的部分,取最大值(因左右两侧都需满足)
public class Candy {
public static int candy(int[] scores, int[] candys) {
if (scores == null || scores.length < 1 || candys.length < scores.length) {
return 0;
}
if (scores.length == 1) {
candys[0] = 1;
}
Arrays.fill(candys, 1);
for (int i = 0; i < scores.length-1; i++) {
if (scores[i] < scores[i + 1]) {
candys[i+1]++;
}
}
for (int i = scores.length - 1; i > 0; i--) {
if (scores[i] < scores[i - 1] && candys[i] >= candys[i - 1]) {
candys[i - 1] = candys[i] + 1;
}
}
int sum = 0;
for (int i = 0; i < candys.length; i++) {
sum += candys[i];
}
return sum;
}
public static void main(String[] args) {
int[] scores1 = {1,2,2};
int[] scores2 = {1,0,2};
int[] candys = new int[scores1.length];
int sum1 = candy(scores1, candys);
// int sum2 = candy(scores2, candys);
System.out.println(Arrays.toString(candys));
System.out.println(sum1);
}
}