C++ Module 02 – Fixed-Point Numbers & Operator Overloading 🔢🧩

✅ Status: Completed – all mandatory exercises (ex03 optional)
🏫 School: 42 – C++ Modules (Module 02)
🏅 Score: 100/100

Ad-hoc polymorphism, operator overloading, and the Orthodox Canonical Class Form (C++98).

---

📚 Table of Contents

• Description

• Goals of the Module

• How Fixed Works (Quick Intuition)

  • Bit Shifts and Powers of Two

• How BSP Works (ex03)

  • BSP
  • Cross Product
  • Right-Hand Rule
  • What the cross Value Means

• Exercises Overview

  • ex00 – My First Class in Orthodox Canonical Form
  • ex01 – Towards a more useful fixed-point number class
  • ex02 – Now we’re talking
  • ex03 – BSP (optional)

• Requirements

• Build & Run

• Repository Layout

• Testing Tips

• 42 Notes

---

📝 Description

This repository contains my solutions to 42’s C++ Module 02 (C++98). The module focuses on building a fixed-point number class, progressively enhancing it with conversions, stream output, comparisons, arithmetic, and increment/decrement operators — all while respecting the Orthodox Canonical Form.

---

🎯 Goals of the Module

Concepts covered:

• Orthodox Canonical Form (default ctor, copy ctor, copy assignment, destructor)
• Operator overloading (<<, comparisons, arithmetic, ++/--, min/max)
• Fixed-point representation and precision behavior (fractional bits)
• Clean separation: headers (.hpp) vs implementation (.cpp)

---

🧠 How Fixed Works (Quick Intuition)

In this module, Fixed stores a real number using an integer internally:

• The internal storage is usually something like int raw.
• The class uses a constant number of fractional bits (in the subject it’s typically 8).
• That means your value is scaled by:

scale = 1 << fractionalBits; // for 8 bits => 1 << 8 == 256

So you can think of it like:

• Real value = raw / 256
• Raw value = real * 256

Examples (with 8 fractional bits):

• 1.0 is stored as 256
• 42.0 is stored as 42 * 256 = 10752
• the smallest step (epsilon) is 1 / 256

That’s also why in ex02 ++fixed increases the value by exactly one epsilon: it increments the raw integer by 1, which corresponds to +1/256.

---

Bit Shifts and Powers of Two

Multiplying by 2^n

For integer values, multiplying by 2^n can be done in several ways.

• Using bitwise left shift (recommended for integers):

int result = x << n; // x * 2^n

• Using the pow function from the <cmath> library (less ideal for integers because it uses floating point):

#include <cmath>

int result = static_cast<int>(x * pow(2, n)); // x * 2^n

• Using a loop:

int result = x;
for (int i = 0; i < n; ++i)
{
    result *= 2; // multiply by 2 each step
}

---

Dividing by 2^n

For positive integers, dividing by 2^n can also be written in several ways.

• Using bitwise right shift (for non-negative integers):

int result = x >> n; // x / 2^n, fractional part is discarded

• Using integer division with a power-of-two factor:

int result = x / (1 << n); // x / 2^n, integer division

• Using a loop:

int result = x;
for (int i = 0; i < n; ++i)
{
    result /= 2; // divide by 2 each step, discarding fractions
}

In summary:

• x << n is equivalent to x * 2^n (for integers without overflow).
• x >> n is roughly equivalent to x / 2^n for non-negative integers, with the fractional part discarded.

🔗 How it maps to Fixed If your Fixed has fractionalBits = 8, then:

• Converting int -> Fixed is basically raw = i << 8
• Converting Fixed -> int is basically i = raw >> 8 (discarding fractions)

---

📐 How BSP Works (ex03)

This section is a practical explanation of the idea behind ex03: checking whether a point P lies strictly inside triangle ABC. In this module we typically use the cross product approach (orientation test).

BSP

BSP (Binary Space Partitioning) is a technique that can be used to determine whether a point P is inside triangle ABC.

How do we determine where P is relative to triangle ABC?

Here’s a great article describing two of the most popular approaches (in English): https://www.sunshine2k.de/coding/java/PointInTriangle/PointInTriangle.html

There are multiple ways to solve the “point in triangle” problem:

• using the cross product of vectors
• using barycentric coordinates
• using triangle areas
• using angles between vectors
• etc.

In this module, we implement the first approach — using the cross product.

---

Cross Product

A point is a position: A(x, y).

A vector is a direction + length, obtained by “going from one point to another”.

Example:

• A(0, 0)
• B(10, 0)

Then vector AB = B - A:

• AB.x = B.x - A.x = 10 - 0 = 10
• AB.y = B.y - A.y = 0 - 0 = 0

So AB = (10, 0) — an arrow pointing right. Similarly:

• AP = P - A
• BC = C - B
• BP = P - B
• etc.

👉 In code, this is typically written like:

Fixed abx = b.getX() - a.getX();
Fixed aby = b.getY() - a.getY();
Fixed apx = p.getX() - a.getX();
Fixed apy = p.getY() - a.getY();

Formula:

cross(AB, AP) = AB.x * AP.y - AB.y * AP.x

The cross product of two vectors is perpendicular to both (in 2D we effectively compute the Z component), and its sign tells us the orientation (clockwise vs counter-clockwise).

---

Right-Hand Rule

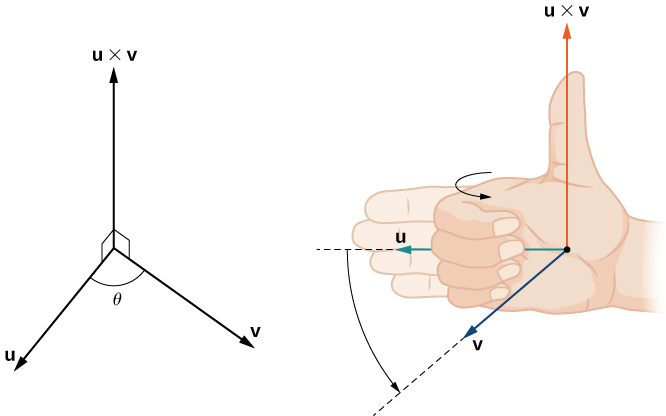
Using the right-hand rule, we can understand where point P lies relative to the directed line AB.

Common right-hand rule variants:

1. Index finger + middle finger RHR (three-finger rule).

2. Curl Fingers RHR (right-hand screw rule).

3. Palm-push RHR (right-hand palm rule).

⚠️ Note: the last image link may expire (it contains a signed URL). If you want long-term stability on GitHub, consider rehosting it or switching to a stable source.

---

What the cross Value Means

This part is the most important:

• The sign tells where P is relative to the directed line AB:

  • cross > 0 → P is on the left side of AB
  • cross < 0 → P is on the right side of AB
  • cross = 0 → P lies on the line AB (on the boundary)

👉 How it’s used for triangle ABC:

• Compute cross(AB, AP), cross(BC, BP), cross(CA, CP)
• If all three have the same sign (and none is 0), then the point is strictly inside
• If any of them is 0, the point is on an edge/vertex → false (per subject: edges/vertices are excluded)

---

📦 Exercises Overview

ex00 – My First Class in Orthodox Canonical Form

Goal: Create a Fixed class (OCF) storing a fixed-point value as an int, with 8 fractional bits stored as a static const int. Add getRawBits() / setRawBits().

---

ex01 – Towards a more useful fixed-point number class

Goal: Add:

• Fixed(int const)
• Fixed(float const)
• toFloat() and toInt()
• operator<< to print float representation

Allowed function: roundf (from <cmath>)

---

ex02 – Now we’re talking

Goal: Add:

• Comparisons: > < >= <= == !=
• Arithmetic: + - * /
• Pre/Post increment & decrement
• Static min / max overloads for const and non-const references

Allowed function: roundf (from <cmath>)

---

ex03 – BSP (optional)

Goal: Implement:

• Point class with const Fixed coordinates
• bsp(a, b, c, point) → true only if point is strictly inside triangle (edges/vertices → false)

---

🛠 Requirements

From the subject:

• Compiler: c++
• Flags: -Wall -Wextra -Werror + -std=c++98
• Forbidden: printf, malloc/alloc, free (and family)
• Also forbidden unless explicitly allowed: using namespace ..., friend
• No STL containers/algorithms until later modules (08/09)

Makefile expectations follow the same rules as in C projects (targets like all/clean/fclean/re, no unnecessary relink, etc.).

---

▶️ Build & Run

git clone <this-repo-url>
cd cpp-module-02

cd ex00 && make && ./a.out
cd ../ex01 && make && ./a.out
cd ../ex02 && make && ./a.out
cd ../ex03 && make && ./a.out   # optional

---

📂 Repository Layout

cpp-module-02/
├── ex00/  (Fixed OCF + raw bits)
├── ex01/  (int/float conversions + operator<<)
├── ex02/  (full operators)
└── ex03/  (Point + bsp)  [optional]

---

🔍 Testing Tips

• Verify that toInt() truncates toward zero (fraction discarded)
• Compare a++ vs ++a
• Validate min/max for const and non-const overloads
• For ex03: points inside/outside/on-edge/on-vertex (edge & vertex must be false)

---

🧾 42 Notes

• C++ modules do not use Norminette; readability still matters for peer evaluation.
• From Module 02 onward, Orthodox Canonical Form is mandatory unless stated otherwise.